NCERT Solutions for Class 10th: Chapter 3 Metals and Non-metals Science
Chapter 3 of Class 10 Science Metals and nonmetals contains Properties of metals and non-metals; Reactivity series; Formation and properties of ionic compounds; Basic metallurgical processes; Corrosion and its prevention. Here, we have provided NCERT Solutions for Chapter 3 Metals and Non-metals which will help the students in learning basics of the lessons. Our experts have tried the best to prepare the questions and answers according to the latest pattern of CBSE.

| Study Reference for Class 10 Chapter 3 Metals and Non-metals |
|---|
|
In Text Questions
Page No: 40
1. Give an example of a metal which
(i) is a liquid at room temperature.
► Mercury
(ii) can be easily cut with a knife.
► Sodium
(iii) is the best conductor of heat.
(iv) is a poor conductor of heat.
► Mercury and Lead
Answer
Malleable:Substances that can be beaten into thin sheets are called malleable. For example, most of the metals are malleable.
Ductile: Substances that can be drawn into thin wires are called ductile. For example, most of the metals are ductile.
Page no: 46
Answer
Sodium is high reactive element. If it is kept in open it can explosively react with oxygen to catch fire. Hence to prevent accidental damage sodium is immersed in kerosene oil.
2. Write equations for the reactions of
(i) iron with steam
(ii) calcium and potassium with water
Answer
(i) 3Fe (s) + 4H2O (g) → Fe3O4 (aq) + 4H2 (g)
(ii) Ca (s) + 2H2O (l) → Ca(OH)2 (aq) + H2 (g) + Heat
2K (s) + 2H2O (l) → 2KOH (aq) + H2 (g) + Heat
3. Samples of four metals A, B, C and D were taken and added to the following solution one by one. The results obtained have been tabulated as follows.
Metal | Iron (II) sulphate | Cooper (II) sulphate | Zinc sulphate | Silver nitrate |
A. | No reaction | Displacement | ||
B. | Displacement | No reaction | ||
C. | No reaction | No reaction | No reaction | Displacement |
D. | No reaction | No reaction | No reaction | No reaction |
Use the Table above to answer the following questions about metals A, B, C and D.
(i) Which is the most reactive metal?
(ii) What would you observe if B is added to a solution of copper (II) sulphate?
(iii) Arrange the metals A, B, C and D in the order of decreasing reactivity.
Answer
(i) B is most reactive metal.
(ii) B will displace copper from copper sulphate.
(iii) Arrangement of metals in the order of decreasing reactivity B>A>C>D.
4. Which gas is produced when dilute hydrochloric acid is added to a reactive metal? Write the chemical reaction when iron reacts with dilute H2SO4.
Answer
Hydrogen gas is evolved when dilute hydrochloric acid is added to a reactive metal.
When iron reacts with dilute H2SO4, iron (II) sulphate with the evolution of hydrogen gas is formed.
Fe (s) + H2SO4 (aq) → FeSO4 (aq) + H2 (g)
5. What would you observe when zinc is added to a solution of iron (II) sulphate? Write the chemical reaction that takes place.
Fe (s) + H2SO4 (aq) → FeSO4 (aq) + H2 (g)
5. What would you observe when zinc is added to a solution of iron (II) sulphate? Write the chemical reaction that takes place.
Answer
When zinc is added to iron (II) sulphate then it will displace the iron from iron sulphate solution as shown in the following chemical reaction.Zn (s) + FeSO4 (aq) → ZnSO4 (aq) + Fe (s)
Page No: 49
1. (i) Write the electron-dot structures for sodium, oxygen and magnesium.
(ii) Show the formation of Na2O and MgO by the transfer of electrons.
(iii) What are the ions present in these compounds?
Answer
(i) The representation of elements with valence electrons as dots around the elements is referred to as electron-dot structure for elements.

(ii)
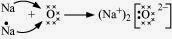
(iii) The ions present in Na2O are Na+ and O2- ions and in MgO are Mg2+ and O2- ions.
2. Why do ionic compounds have high melting points?
Answer
Ionic compounds have strong electrostatic forces of attraction between the ions. Therefore, it requires a lot of energy to overcome these forces. That is why ionic compounds have high melting points.
Page No: 53
1. Define the following terms.
(i) Mineral (ii) Ore (iii) Gangue
(i) Mineral (ii) Ore (iii) Gangue
Answer
(ii) Ore: Minerals from which metals can be extracted profitably are known as ores.
(iii) Gangue: The impurities present in the ore such as sand, rocks etc are non as gangue.
2. Name two metals which are found in nature in the free state.
Answer
The metals at the bottom of the reactivity series are mostly found in free state. For example: gold, silver, and platinum.
3. What chemical process is used for obtaining a metal from its oxide?
Answer
A metal can be extracted from its oxide by the process of reduction.
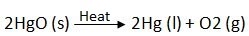
Page No: 55
1. Metallic oxides of zinc, magnesium and copper were heated with the following metals.
| Metal | Zinc | Magnesium | Copper |
| Zinc oxide | - | - | - |
| Magnesium oxide | - | - | - |
| Copper oxide | - | - | - |
In which cases will you find displacement reactions taking place?
Answer
| Metal | Zinc | Magnesium | Copper |
| Zinc oxide | No reaction | Displacement | No reaction |
| Magnesium oxide | No reaction | No reaction | No reaction |
| Copper oxide | Displacement | Displacement | No reaction |
2. Which metals do not corrode easily?
Answer
Metals which have low reactivity such as silver, gold does not corrode easily.
3. What are alloys?
Answer
An alloy is the homogeneous mixture of two or more metals or metals and non metals. For example brass is an alloy of copper and zinc.
Page No: 56
Excercise
1. Which of the following pairs will give displacement reactions?
(a) NaCl solution and copper metal
(b) MgCl2solution and aluminium metal
(c) FeSO4solution and silver metal
(d) AgNO3solution and copper metal.
► (d) AgNO3solution and copper metal.
2. Which of the following methods is suitable for preventing an iron frying pan from rusting?
(a) Applying grease
(b) Applying paint
(c) Applying a coating of zinc
(d) all of the above.
► (c) Applying a coating of zinc
3. An element reacts with oxygen to give a compound with a high melting point. This compound is also soluble in water. The element is likely to be
(a) calcium
(b) carbon
(c) silicon
(d) iron
► (a) calcium
4. Food cans are coated with tin and not with zinc because
(a) zinc is costlier than tin.
(b) zinc has a higher melting point than tin.
(c) zinc is more reactive than tin.
(d) zinc is less reactive than tin.
► (c) zinc is more reactive than tin.(d) zinc is less reactive than tin.
5. You are given a hammer, a battery, a bulb, wires and a switch.
(a) How could you use them to distinguish between samples of metals and non-metals?
(b) Assess the usefulness of these tests in distinguishing between metals and non-metals.
(b) Assess the usefulness of these tests in distinguishing between metals and non-metals.
Anwer
(a) With the hammer, we can beat the sample and if it can be beaten into thin sheets (that is, it is malleable), then it is a metal otherwise a non-metal. Similarly, we can use the battery, bulb, wires, and a switch to set up a circuit with the sample. If the sample conducts electricity, then it is a metal otherwise a non-metal.
(b) The above tests are useful in distinguishing between metals and non-metals as these are based on the physical properties. No chemical reactions are involved in these tests.
Answer
Those oxides that behave as both acidic and basic oxides are called amphoteric oxides.
Examples: aluminium oxide (Al2O3), zinc oxide (ZnO)
7. Name two metals which will displace hydrogen from dilute acids, and two metals which will not.
Examples: aluminium oxide (Al2O3), zinc oxide (ZnO)
7. Name two metals which will displace hydrogen from dilute acids, and two metals which will not.
Answer
Iron and aluminium will displace hydrogen from dilute acids as they more reactive then hydrogen. Mercury and copper cannot displace hydrogen from dilute acids as they are less reactive than hydrogen.
Page No: 57
8. In the electrolytic refining of a metal M, what would you take as the anode, the cathode and the electrolyte?
Answer
In the electrolytic refining of a metal M:
Anode → Impure metal M
Cathode → Thin strip of pure metal M
Electrolyte → Solution of salt of the metal M
9. Pratyush took sulphur powder on a spatula and heated it. He collected the gas evolved by inverting a test tube over it, as shown in figure below.
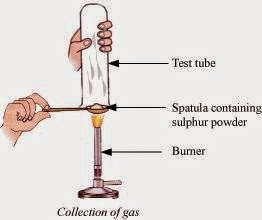
(i) dry litmus paper?
(ii) moist litmus paper?
(b) Write a balanced chemical equation for the reaction taking place.
Answer
(a)
(i) There will be no action on dry litmus paper.
(ii) The colour of litmus paper will turn red because sulphur is a non-metal and the oxides of non-metal are acidic in nature.
(ii) The colour of litmus paper will turn red because sulphur is a non-metal and the oxides of non-metal are acidic in nature.
(b) S (s) + O2(g) → SO2 (g)
10. State two ways to prevent the rusting of iron.
Answer
Two ways to prevent the rusting of iron are:
→ Oiling, greasing, or painting: By applying oil, grease, or paint, the surface becomes water proof and the moisture and oxygen present in the air cannot come into direct contact with iron. Hence, rusting is prevented.
→ Galvanisation:An iron article is coated with a layer of zinc metal, which prevents the iron to come in contact with oxygen and moisture. Hence, rusting is prevented.
11. What type of oxides are formed when non-metals combine with oxygen?
Answer
When non-metals are combined with oxygen then neutral or acidic oxides are formed. Examples of acidic oxides are NO2, SO2 and examples of neutral oxides are NO, CO etc.
12. Give reasons
(a) Platinum, gold and silver are used to make jewellery.
(b) Sodium, potassium and lithium are stored under oil.
(c) Aluminium is a highly reactive metal, yet it is used to make utensils for cooking.
(d) Carbonate and sulphide ores are usually converted into oxides during the process of extraction.
(c) Aluminium is a highly reactive metal, yet it is used to make utensils for cooking.
(d) Carbonate and sulphide ores are usually converted into oxides during the process of extraction.
Answer
(a) Platinum, gold, and silver are used to make jewellery because they are very lustrous. Also, they are very less reactive and do not corrode easily.
(b) Sodium, potassium, and lithium are very reactive metals and react very vigorously with air as well as water.Therefore, they are kept immersed in kerosene oil in order to prevent their contact with air and moisture.
(c) Though aluminium is a highly reactive metal, it is resistant to corrosion. This is because aluminium reacts with oxygen present in air to form a thin layer of aluminium oxide. This oxide layer is very stable and prevents further reaction of aluminium with oxygen. Also, it is light in weight and a good conductor of heat. Hence, it is used to make cooking utensils.
(d) Carbonate and sulphide ores are usually converted into oxides during the process of extraction because metals can be easily extracted from their oxides rather than from their carbonates and sulphides.
13. You must have seen tarnished copper vessels being cleaned with lemon or tamarind juice. Explain why these sour substances are effective in cleaning the vessels.
Answer
Copper reacts with moist carbon dioxide in air to form copper carbonate and as a result, copper vessel loses its shiny brown surface forming a green layer of copper carbonate. The citric acid present in the lemon or tamarind neutralises the basis copper carbonate and dissolves the layer. That is why, tarnished copper vessels are cleaned with lemon or tamarind juice to give the surface of the copper vessel its characteristic lustre.
14. Differentiate between metal and non-metal on the basis of their chemical properties.
Answer
Metal | Non-metal |
| Metals are electropositive. | Non-metals are electronegative. |
| Oxides of metal are basic in nature. | Oxides of non-metals are acidic in nature. |
| Metals displace hydrogen from dilute acids. | They can't replace hydrogen from dilute acids. |
| Metals form chlorides which are electrovalent or ionic compounds. | Non-metals form chlorides which are covalent compounds. |
| They react with water to form oxides and hydroxides. Some metals react with cold water, some with hot water, and some with steam. | They do not react with water. |
15. A man went door to door posing as a goldsmith. He promised to bring back the glitter of old and dull gold ornaments. An unsuspecting lady gave a set of gold bangles to him which he dipped in a particular solution. The bangles sparkled like new but their weight was reduced drastically. The lady was upset but after a futile argument the man beat a hasty retreat. Can you play the detective to find out the nature of the solution he had used?
Answer
The solution he had used was Aqua regia. Aqua regia is Latin word which means ‘Royal Water’. It is the mixture of concentrated Hydrochloric acid and concentrated nitric acid in the ratio of 3:1. It is capable of dissolving metals like Gold and Platinum. Since the outer layer of the gold bangles is dissolved in aqua regia so their weight was reduced drastically.
16. Give reasons why copper is used to make hot water tanks and not steel (an alloy of iron).
Answer
Copper does not react with cold water, hot water, or steam. However, iron reacts with steam. If the hot water tanks are made of steel (an alloy of iron), then iron would react vigorously with the steam formed from hot water. 3Fe + 4H2O → Fe3O4 + H2O
That is why copper is used to make hot water tanks, and not steel.
Why do silver articles become black after sometime when exposed to air?They get tarnished by reacting with atmospheric air to form silver sulphide. Which gas is usually liberated when an acid reacts with a metal?
Hydrogen gas Name the metal which react with a very dilute HNO3 to evolve hydrogen gas
Manganese or MagnesiumWhy does calcium floats on water?
Calcium floats on water because the bubbles of hydrogen gas formed and stick to the surface of calcium metal. In the formation of a compound X, Yatom 'X' gives one electron to an atom of 1'. What is the nature of bond in XY?
Ionic Bond
Go Back To NCERT Solutions for Class 10th Science
They get tarnished by reacting with atmospheric air to form silver sulphide.
Which gas is usually liberated when an acid reacts with a metal?
Hydrogen gas
Name the metal which react with a very dilute HNO3 to evolve hydrogen gas
Manganese or Magnesium
Why does calcium floats on water?
Calcium floats on water because the bubbles of hydrogen gas formed and stick to the surface of calcium metal.
In the formation of a compound X, Yatom 'X' gives one electron to an atom of 1'. What is the nature of bond in XY?
Ionic Bond
Go Back To NCERT Solutions for Class 10th Science


































