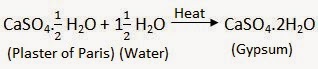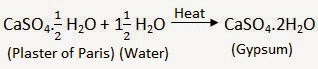OJEE 2020 Application process begins, Exam To Be Held In first week of May

February 6, 2020, 3:55 am

≫ Next: Use CBSE Exam Locator App to find your exam center

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.1

OJEE 2020 Application process begins at ojee.nic.in, Exam To Be Held In first week of May

As pert the latest information, OJEE committee has decided to conduct Odisha Joint Entrance Examination (OJEE) in the first week of May. OJEE is a computer based exam conducted for admission to Undergraduate Courses (lateral entry) Engineering and Technology, and Postgraduate Courses like MBA, MCA (lateral entry), MCA, MTECH, MPLAN, MARCH, MPHARM, and Int. MBA in Universities, Govt. Colleges, and Self-financed institutions in the State.

You can apply for OJEE 2020 by clicking here.

Different forms are present for different types of entrance exams. You need to select according to your qualification.

The official notification released by OJEE states that "Please note that outside state candidates are not eligible for admission in government colleges, but they are eligible for admission in private colleges as per Odisha government rule," said the OJEE committee in the official notification."

OJEE Eligibility Criteria

UG courses- Candidate must have passed Class XII or any equivalent examination. The minimum age of the candidate is 17 years while there is no specified upper age limit.
PG courses- Candidate must have passed the Bachelor’s degree. The minimum age required to apply is 21 years. There is no specified upper age limit.
Lateral Entry courses- Candidate must have passed Diploma or degree program. There are no specified age requirements mentioned by OJEE Board for these courses.

Last year, cyclonic storm Fani has disturbed the OJEE dates. The exam was held on June 8 and June 9 in which total of 25,731 candidates had appeared for the entrance test offline while 13,918 students gave the exam in online mode.

↧

Use CBSE Exam Locator App to find your exam center

February 6, 2020, 4:45 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.2

≪ Previous: OJEE 2020 Application process begins, Exam To Be Held In first week of May

Use CBSE Exam Locator App to find your exam center

CBSE will start conducting the CBSE 10th 12th Board Exam 2020 from February 15, 2020. The board has released the admit cards. Now students can collect their admit card from their respective schools. The admit card will provide students with details like subject code, center name and code etc.

To ease the process of finding exam center, CBSE released an android based mobile app known as Exam Centre Locator App which will help you in finding the exam center. A student can access this application on Google Playstore as CBSE ECL app. CBSE exam locator app was launched on February 14, 2019. Now, you can access it for 2020 board exams.

Steps to use CBSE Exam Locator App

You can go to Play Store application on android phone and search CBSE ECL app there. Also, you can use the direct link to go to CBSE ECL App.
After installing the app, you need to register with the app. In order to do this, use your mobile number and enter the OTP received to register on the app.
Select your exam, Class 10 or Class 12 from the dropdown menu and enter your roll number and click on search.

This year several Principals will be appointed for the duties of Centre Superintendent to supervise Online Exam Centre Management System (OECMS). The OECAMS will be accessible between the month of February to April 2020 which will let you check real-time information like absentee students, invigilators available, PwD, scribe, unfair means, feedback about the question papers etc.

Also, to help students in dealing with exam stress, CBSE has started free psychological counselling session. This is the 23rd consecutive year of this free session.

Class 10 exams will end on March 20 while the class 12 exams will end on March 30.

↧

NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.2

February 6, 2020, 8:35 am

≫ Next: NCERT Solutions for Class 8th: Ch 15 Introduction to Graphs Geometry

≪ Previous: Use CBSE Exam Locator App to find your exam center

NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.2

Chapter 13 Limits and Derivatives Exercise 13.2 NCERT Solutions for Class 11 Maths will help you in solving your doubts as these Class 11 Maths NCERT Solutions are prepared by Studyrankers experienced subject matter experts. These NCERT Solutions are very important for the purpose of examinations as it will help you knowing the basic concepts of the chapter.

1. Find the derivative of x² – 2 at x = 10

Answer

Let y = x² – 2
dy/dx = 2x dy/dx at x = 10 is equal to 20

2. Find the derivative of x 2 – 2 at x = 10
Find the derivative of 99x at x = 100 (By first principle)

Answer

Let f (x) = 99x. Derivative of f (x) at x = 100 is

Now, f (x) = 99x
f (100 + h)= 99(100 + h)
f (100)= 99 × 100
∴ f (100 + h) – f (100) = 99 (100 + h) – 99 × 100
= 99 [100 + h – 100] = 99 × h

3. Find the derivative of x at x = 1

Answer

Derivative of f (x) = x at x = 1

4. Find the derivative of the following functions from first principle:
(i) x ³ – 27 (ii) (x – 1)(x – 2)
(iii) 1/x² (iv) (x + 1)/(x – 1)

Answer

5. For the function
f(x) = x¹⁰⁰/100 + x⁹⁹/99 + ……..+ x²/2 + x + 1
prove that f’(1) = 100 f’(0)

Answer

We know that d/dx (xⁿ) = nx^n-1
∴ For f(x) = x¹⁰⁰/100 + x⁹⁹/99 + ……+ x²/2 + x+ 1
f'(x) = 100x⁹⁹/100 + 99. x⁹⁸/99 + …..+ 2x/2 + 1
= x⁹⁹ + x⁹⁸ + ………….+ x + 1
Now, f’(x) = 1 + 1+ …….. to 100 term = 100
f'(0) = 1
∴ f'(1) = 100 × 1 = 100f’(0)
hence, f’(1) = 100f’(0)

6. Find the derivative of xⁿ + ax^{n – 1} + a ²x ^{n – 2} + ....+ a ^{n –} ¹x + aⁿ for some fixed real number a?

Answer

Let f (x) = xⁿ + ax^{n – 1} + a² x ⁿ ^{– 2}+ ........ + a ^{n –} ¹x + aⁿ
Now, d/dx xⁿ = nx^n-1, d/dx x^n-1= (n – 1)x^n-2.
etc and d/dx [ag(x)] = ag’(x), d/dx aⁿ = 0
f’(x) = nx^n-1+ (n – 1)ax^{n – 2}+ (n – 2)a²x^n-3+ ………..+ a^n-1

7. For some constants a and b, find the derivative of:
(i) (x – a)(x – b)
(ii) For some constant a and b find the derivation of (ax² + b)² .
(iii) (x – a)/( x – b)

Answer

(i) Let f (x) = (x – a)(x – b)
Using product rule, we have
df(x)/dx = (x – a) d(x – b)/dx + (x-b) d(x-a)/dx
= (x – a)[d(x)/dx - d(b)/dx] + (x – b)[d(x)/dx - d(a)/dx]
= (x – a)[1 – 0] + (x – b)[1 – 0]
(ii) f(x) = (ax² + b)² = a²x⁴+ 2abx² + b²
now, d/dx x⁴ = 4x³ and
d/dx x² = 2x, d/dx b² = 0
f’(x) = a². 4x³ + 2ab.2x + 0
= 4a²x³ + 4abx
(iii) Let f(x) = (x- a)/(x – b)
Using quotient rule, we have
= ((x – b)(d(x-a))/dx – (x – a) (d(x – b))/dx)/(x – b)²

8. Find the derivative of (xⁿ – aⁿ)/(x – a) for some constant ‘a’.

Answer

We know d/dx (u/v) = (u’v – uv’)/v²
d/dx ((xⁿ – aⁿ)/(x – a))
= ([d/dx (xⁿ – aⁿ)](x – a)-(xⁿ – aⁿ)d/dx (x – a))/(x – a)²
= (nx^n-1(x – a)- (xⁿ – aⁿ). 1)/(x – a)²
= (nxⁿ – n.x^{n – 1}a – xⁿ + aⁿ)/(x – a)²
= ((n – 1 )xⁿ – nax^n-1+ aⁿ)/(x – a)²

9. Find the derivative of
(i) 2x – 3/4
(ii) (5x³ + 3x – 1)(x – 1)
(iii) x^-3(5 + 3x)
(iv) x⁵(3 – 6x^-9)
(v) x^-4(3 – 4x^-5)
(vi) 2/(x + 1) - x²/(3x – 1)

Answer

(i) Let f(x) = 2x – 3/4
f'(x) = 2 (d/dx) x = 1, (d/dx)(3/4) = 0

(ii) let f(x) = (5x3 + 3x – 1)(x – 1)
(uv)’ = u’v + uv’
f'[(5x3 + 3x – 1)(x – 1)]
= [d/dx (5x³ + 3x – 1)](x – 1) + (5x³ + 3x – 1) d/dx (x – 1)
= (15x² + 3)(x – 1) + (15x³ + 3x – 1).1
= x(15x² + 3) – (15x² + 3) + (5x³ + 3x – 1))
= 20x³ – 15x² + 6x - 4

(iii) let f(x) = x^-3 (5 + 3x) = 5x^-3+ 3x^-2
f’(x) = 5(-3)x^-4+ 3(-2)x^-3
= (-15/x⁴) – (6/x³) = (-(6x + 15))/x⁴ = (-3(2x + 5))/x⁴
(iv) Let f(x) = x⁵(3 – 6x^-9) = 3x⁵ – 6x^-4
f'(x) = (d(3x⁵ – 6x^-4))/dx
= (d(3x⁵)/dx) – (d(6x^-4)/dx)
= 3.(dx⁵/dx) – 6.(dx^-4/dx)
= (3)(5)x⁴ – (6)(-4)x^-5
= 15x⁴ + 24x^-5

(v) let f(x) = x^-4(3 – 4x^-5)
f'(x) = x^-4 . (d(3 – 4x^-5)/dx) + (3 – 4x^-5)(dx^-4/dx)
= x^-4[(d(3)/dx) – (d(4x^-5)/dx)] + (3 – 4x^-5)(-4)x^-5
= x^-4[0 – (4)(-5)x^-6] + (3 – 4x^-5)(-4)x^-5
= x^-4[20x^-6]-x^-5(12 – 16x^-5)
= 20x^-10 – 12x^-5 + 16x^-10 = 36x¹⁰ – 12x^-5

10. Find the derivative of cos x from first principle.

Answer

f (x) = cos x By first Principle,

11. Find the derivative of the following functions:
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi) 5 sin x – 6 cos x + 7
(vii) 2tanx – 7 sec x

Answer

(i) Let f(x) = sinx cosx
f’(x) = u’v + uv’
= (d/dx sin x) cosx + sinx d/dx (cos x)
= cos x. cos x + sin x(-sin x)
cos²x – sin²x = cos2x

(ii)

(iii) Let f(x) = 5secx + 4cos x
f’(x) = (d(5sec x + 4cos x))/dx
= (d(5sec x)/dx) + (d(4cosx)/dx)
= 5.(d(sec x)/dx) + 4.(d(cos x)/dx)
= 5sec x tan x – 4 sin x
(iv) Let f(x) = cosec x
f'(x) = (d(cosec x))/dx = (d. 1/sinx)/dx
= (sinx (d(1)/dx) – (1.d(sin x)/dx))/(sin x)²
= (0 – cos x)/(sin² x) = (-cosx/sin x). (1/sin x)
= - cosec x cot x
(v) Now,
d/dx (3 cot x) = 3. d/dx (cot x) = -3 cosec² x
Also, 5.d/dx (cosec x) = - 5cosec x cot x
d/dx (3cot x + 5 cosec x)
= -3 cosec²x – 5cosec x cot x
= -cosec x (3cosec x + 5 cot x)
(vi) Let f(x) = 5 sin x – 6 cos x + 7
f'(x) = (d(5 sin x – 6 cos x + 7))/dx
= (d(5 sin x))/dx - (d(6 cos x))/dx + (d(7))/dx
= 5cos x – 6(- sin x) + 0
= 5 cos x + 6 sin x

↧

NCERT Solutions for Class 8th: Ch 15 Introduction to Graphs Geometry

February 6, 2020, 9:20 am

≫ Next: NCERT Solutions for Class 8th: Ch 16 Playing with Numbers Geometry

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.2

NCERT Solutions for Chapter 14 Factorisation Class 8 Mathematics

Page No: 236

Exercise 15.1

1. The following graph shows the temperature of a patient in a hospital, recorded every hour:
(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5° C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patients’ temperature showed an upward trend?

Answer

(a) The patient’s temperature was 36.5o C at 1 p.m.
(b) The patient’s temperature was 38.5o C at 12 noon.
(c) The patient’s temperature was same at 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. is 36.5o C. The point between 1 p.m. and 2 p.m., x-axis is equidistant from the two points showing 1 p.m. and 2 p.m. So, it represents 01.30 p.m. Similarly, the point on y-axis, between 36o C and 37o C will represent 36.5o C.
(e) The patient’s temperature showed an upward trend from 9 a.m. to 11 a.m., 11 a. m. to 12 noon and 2 p.m. to 3 p.m.

2. The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in (i) 2002 (ii) 2006?
(b) What were the sales in (i) 2003 (ii) 2005?
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared
to its previous year?

Answer

(a) The sales in: (i) 2002 was Rs.4 crores and (ii) 2006 was Rs.8 crores.
(b) The sales in: (i) 2003 was Rs.7 crores (ii) 2005 was Rs.10 crores.
(c) The difference of sales in 2002 and 2006 = Rs.8 crores – Rs.4 crores = Rs.4 crores
(d) In the year 2005, there was the greatest difference between the sales as compared to its previous year, which is (Rs.10 crores – Rs.6 crores) = Rs.4 crores.

3. For an experiment in Botany, two different plants, plant A and plant B were grownunder similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.
(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks?
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks?
(c) How much did Plant A grow during the 3rd week?
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.

Answer

(a) (i) The plant A was 7 cm high after 2 weeks and
(ii) after 3 weeks it was 9 cm high.

(b) (i) Plant B was also 7 cm high after 2 weeks and
(ii) after 3 weeks it was 10 cm high.

(c) Plant A grew = 9 cm – 7 cm = 2 cm during 3rd week.

(d) Plant B grew during end of the 2nd week to the end of the 3rd week = 10 cm – 7 cm = 3 cm.

(e) Plant A grew the highest during second week.

(f) Plant B grew the least during first week.

(g) At the end of the second week, plant A and B were of the same height.

4. The following graph shows the temperature forecast and the actual temperature for each day of a week.
(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?

Answer

(a) On Tuesday, Friday and Sunday, the forecast temperature was same as the actual temperature.
(b) The maximum forecast temperature was 35o C.
(c) The minimum actual temperature was 15o C.
(d) The actual temperature differed the most from the forecast temperature on Thursday.

5. Use the tables below to draw linear graphs.

Year	2003	2004	2005	2006
Days	8	10	5	12

(a) The number of days a hill side city received snow in different years.

Year	2003	2004	2005	2006	2007
No. of Men	12	12.5	13	13.2	13.5
No. of Women	11.3	11.9	13	13.6	12.8

(b) Population (in thousands) of men and women in a village in different years.

Answer

(a)

(b)

6. A courier-person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

Answer

(a) 4 units = 1 hour.
(b) The person took 3.1/2 hours for the travel.
(c) It was 22 km far from the town.
(d) Yes, this has been indicated by the horizontal part of the graph. He stayed from 10 am to 10.30 am.
(e) He rode the fastest between 8 am and 9 am.

7. Can there be a time-temperature graph as follows? Justify your answer.

Answer

(i) It is showing the increase in temperature.
(ii) It is showing the decrease in temperature.
(iii) The graph figure (iii) is not possible since temperature is increasing very rapidly which is not possible.
(iv) It is showing constant temperature.

Page No. 243

Exercise 15.2

1. Plot the following points on a graph sheet. Verify if they lie on a line
(a) A(4,0), B(4,2), C(4,6), D(4, 2.5)
(b) P(1,1), Q(2,2), R(3,3), S(4,4)
(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5)

Answer

(a) All points A, B, C and D lie on a vertical line.
(b) P, Q, R and S points also make a line. It verifies that these points lie on a line.
(c) These points do not lie in a straight line.

2. Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and y-axis.

Answer

The coordinates of the points at which this line meets the x-axis at (5, 0) and y-axis at (0, 5).

3. Write the coordinates of the vertices of each of these adjoining figures.

Answer

Vertices of figure OABC
O (0, 0), A (2, 0), B (2, 3) and C (0, 3)
Vertices of figure PQRS
P (4, 3), Q (6, 1), R (6, 5) and S (4, 7)
Vertices of figure LMK
L (7, 7), M (10, 8) and K (10, 5)

4. State whether True or False. Correct that are false.
(i) A point whose x coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
(ii) A point whose y coordinate is zero and x-coordinate is 5 will lie on y-axis.
(iii) The coordinates of the origin are (0, 0).

Answer

(i) True

(ii) False, it will lie on x-axis.

(iii) True

Page No. 247

Exercise 15.3

1. Draw the graphs for the following tables of values, with suitable scales on the axes.
(a) Cost of apples

No. of apples	1	2	3	4	5
Cost (in Rs.)	5	10	15	20	25

(b) Distance travelled by a car

Time (in hours)	6 a.m.	7 a.m.	8 a.m.	9 a.m.
Distance (in km)	40	80	120	160

(i) How much distance did the car cover during the period 7.30 a.m. to 8 a.m?
(ii) What was the time when the car had covered a distance of 100 km since it’s start?
(c) Interest on deposits for a year.

Deposit(inRs.)	1000	2000	3000	4000	5000
Simple Interest (inRs.)	80	160	240	320	400

(i) Does the graph pass through the origin?
(ii) Use the graph to find the interest on Rs 2500 for a year.
(iii) To get an interest of Rs 280 per year, how much money should be deposited?

Answer

(a)

(b) (i) The car covered 20 km distance.
(ii) It was 7.30 am, when it covered 100 km distance.

(c) (i) Yes, the graph passes through the origin.
(ii) Interest on Rs. 2500 is Rs. 200 for a year.
(iii) Rs. 3500 should be deposited for interest of Rs. 280.

2. Draw a graph for the following.
(i)

Side of Square(in cm)	2	3	3.5	5	6
Perimeter (in cm)	8	12	14	20	24

Is it a linear graph?
(ii)

Side of Square(in cm)	2	3	4	5	6
Area (in cm2)	4	9	16	25	36

Is it a linear graph?

Answer

(i) Yes, it is a linear graph.

(ii) No, it is not a linear graph because the graph does not provide a straight line.

Go to Chapters list NCERT Solutions of Class 8 Maths

↧

NCERT Solutions for Class 8th: Ch 16 Playing with Numbers Geometry

February 6, 2020, 10:46 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.1

≪ Previous: NCERT Solutions for Class 8th: Ch 15 Introduction to Graphs Geometry

NCERT Solutions for Chapter 16 Playing with Numbers Class 8 Mathematics

Page No: 220

Exercise 16.1

Find the values of the letters in each of the following and give reasons for the steps involved.

1.

Answer

On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get, 7 + 5 = 12 in which ones place is 2.
∴ A = 7
And putting 2 and carry over 1, we get
B = 6
Hence A = 7 and B = 6

2.

Answer

On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get,8 + 5 = 13 in which ones place is 3.
∴ A = 5
And putting 3 and carry over 1, we get
B = 4 and C = 1
Hence A = 5, B = 4 and C = 1

3.

Answer

On putting A = 1, 2, 3, 4, 5, 6, 7 and so on and we get, A x A = 6 x 6 = 36 in which ones place is 6.
∴ A = 6
Hence A = 6

4.

Answer

Here, we observe that B = 5
So that 7 + 5 = 12.
Putting 2 at ones place and carry over 1 and A = 2, we get
2 + 3 + 1 = 6
Hence A = 2 and B = 5

5.

Answer

Here on putting B = 0,
we get 0×3 = 0.
And A = 5, then 5×3 = 15
⇒ A = 5 and C = 1
Hence A = 5, B = 0 and C = 1

6.

Answer

On putting B = 0, we get 0 , and A = 5, then 5× 5 = 25
⇒ A = 5, C = 2
Hence A = 5, B = 0 and C = 2

7.

Answer

Here product of B and 6 must be same as ones place digit as B.
6 × 1 = 6, 6 × 2 = 12, 6 × 3 = 18,
6 × 4 = 24
On putting B = 4, we get the ones digit 4 and remaining two B’s value should be 44.
∴ For 6 × 7 = 42 and carry over 2 = 44
Hence A = 7 and B = 4

8.

Answer

On putting B = 9, we get 9 + 1 = 10
Putting 0 at ones place and carry over 1, we get
For A = 7 ⇒ 7 + 1 + 1 = 9
Hence A = 7 and B = 9

9.

Answer

On putting B = 7,
⇒ 7 + 1 = 8
Now A = 4, then 4 + 7 = 11
Putting 1 at tens place and carry over 1, we get
2 + 4 + 1 = 7
Hence A = 4 and B = 7

10.

Answer

Putting A = 8 and B = 1, we get
8 + 1 = 9
Now again we add 2 + 8 = 10
Tens place digit is ‘0’ and carry over 1.
Now 1 + 6 + 1 = 8 = A
Hence A = 8 and B = 1

Page No. 260

Exercise 16.2

1. If 21y5 is a multiple of 9, where y is a digit, what is the value of y?

Answer

Since 21y5 is a multiple of 9.
Therefore according to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
∴ 2+2+y+5= 8+y
⇒ 8+y = 9
⇒ y = 1
Since 21y5 is a multiple of 9.

2. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? You will find that there are two answers for the last problem. Why is this so?

Answer

Since 31z5 is a multiple of 9.
Therefore according to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
∴ 3+1+z+5 = 9+z
⇒ 9+z = 9
⇒ z= 0
If 3 +1+z+5 = 9+z
⇒ 9+a = 18
⇒ z= 9
Hence, 0 and 9 are two possible answers.

3. If 24x is a multiple of 3, where x is a digit, what is the value of x?
(Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers: 0, 3, 6, 9, 12, 15, 18, ... But since x is a digit, it can only be that 6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.)

Answer

Since, 24x is a multiple of 3.
Therefore according to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
∴ 2+4+x = 6 +x
Since x is a digit.
⇒6+x= 6 ⇒ x= 0
⇒ 6+x = 9 ⇒ x= 3
⇒ 6+ x = 12 ⇒x= 6
⇒ 6+x = 15 ⇒ x = 9
Thus, x can have any of four different values.

4. If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?

Answer

Since 31z5 is a multiple of 3.
Therefore according to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
Since z is a digit.
∴ 3+1+z+5 = 9+z
⇒ 9+z=9 ⇒ z= 0
If 3+1+z+5 = 9+z
⇒ 9 +z = 12 ⇒ z= 3
If 3+1+z+5 = 9+z
⇒ 9 + z= 15 ⇒ z= 6
If 3+1+z+5 = 9+z
⇒ 9 +z = 18 ⇒ z= 9
Hence 0, 3, 6 and 9 are four possible answers.

Go to Chapters list NCERT Solutions of Class 8 Maths

↧

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.1

February 7, 2020, 12:00 am

≫ Next: NCERT Solutions for Class 7th: Ch 1 Integers Math

≪ Previous: NCERT Solutions for Class 8th: Ch 16 Playing with Numbers Geometry

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.1

Here you will find the NCERT Solutions of Chapter 14 Mathematical Reasoning Exercise 14.1 will help you in finding solutions of difficult questions. Class 11 Maths NCERT Solutions provided here are prepared by subject matter experts of Studyrankers. It will help you in improving your marks in the examinations and knowing the basic concepts of the chapter.

1. Which of the following sentences are statements? Give reasons for your answer.

(i) There are 35 days in a month.

(ii) Mathematics is difficult.

(iii) The sum of 5 and 7 is greater than 10.

(iv) The square of a number is an even number.

(v) The sides of a quadrilateral have equal length.

(vi) Answer this question.

(vii) The product of (– 1) and 8 is 8.

(viii) The sum of all interior angles of a triangle is 180º.

(ix) Today is a windy day.

(x) All real numbers are complex numbers.

Answer

(i) The given sentence is always false because the maximum number of days in a month is 31. Therefore, it is a statement.

(ii) The given sentence is not a statement because for some people Mathematics can be easy and for some other, it can be difficult.

(iii) Statement: It true that the sum of 5 and 7 is greater than 10.

(iv) Sentence: The square of a number may be even or it may be odd. e.g. 22 = 4 (even), 32 = 9 (odd). (v) Sentence: A quadrilateral may have equal lengths as it may be a rhombus or a square or the quadrilateral may have unequal sides.

(vi) Sentence: It is an order.

(vii) Statement: It is false because product of (–1) and 8 is not 8.

(viii) This sentence is always true and therefore, it is a statement.

(ix) Sentence: It is a windy day which day it is?

(x) Statement: It is true that all real numbers are complex number of the form a + i.

2. Give three example of sentences which are not statements. Give reasons for the answers.

Answer

(i) It is a rainy month. We can not say which month is rainy.

(ii) She is very beautiful. Who is beautiful?

(iii) You are a brave boy. Who is brave?

↧

NCERT Solutions for Class 7th: Ch 1 Integers Math

February 7, 2020, 12:45 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.2

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.1

NCERT Solutions for Chapter 1 Integers Class 7 Mathematics

Page No: 3

Try these

We have done various patterns with numbers in our previous class. Can you find a pattern for each of the following? If yes, complete them:

(a) 7, 3, – 1, – 5, _____, _____, _____.
(b) – 2, – 4, – 6, – 8, _____, _____, _____.
(c) 15, 10, 5, 0, _____, _____, _____.
(d) – 11, – 8, – 5, – 2, _____, _____, _____.
Make some more such patterns and ask your friends to complete them.

Answer

(a) 7, 3, -1, -5, -9, -13, -17
(b) -2, -4, -6, -8, -10, -12, -14
(c) 15, 10, 5, 0, -5, -10, -15
(d) -11, -8, -5, -2, -1, -4, -7

Page No: 4

Exercise 14.1

1. Following number line shows the temperature in degree celsius (°C) at different places on a particular day.

(a) Observe this number line and write the temperature of the places marked on it.

(b) What is the temperature difference between the hottest and the coldest places among the above

(d) Can we say temperature of Srinagar and Shimla taken together is less than the temperature at Shimla? Is it also less than the temperature at Srinagar?

Answer

(a) The temperatures of the places marked on number line are:

Lahulspiti : -8⁰C

Srinagar : -2⁰C

Shimla : 5⁰C

Ooty : 14⁰C

Bangalore : 22⁰C

(b) Temperature at the hottest place = 22⁰C

Temperature at the coldest place = -8⁰C

The temperature difference between these places = 22⁰C - (-8⁰C) = 30⁰C

The temperature at Srinagar = -2⁰C

The temperature difference between these= -8⁰C - (-2⁰C) = -6⁰C

(d) Temperature of Srinagar= -2⁰C

Temperature of Shimla = 5⁰C

Temperature of Srinagar and Shimla taken together = -2⁰C + 5⁰ = 3⁰C

Therefore: 3⁰C < 5⁰C

Yes, we can say that temperature of Srinagar and Shimla taken together is less than the temperature at Shimla.

However, 3⁰C > -2⁰C

Thus, the temperature at Srinagar is not less than the temperature at Shimla.

2. In a quiz, positive marks are given for correct answers and negative marks are given for incorrect answers. If Jack’s scores in five successive rounds were 25, –5, –10, 15 and 10, what was his total at the end?

Answer

Jack’s scores in five successive rounds were 25, -5, -10, 15 and 10.

His total at the end = 25 – 5 – 10 + 15 + 10 = 35

3. At Srinagar temperature was – 5°C on Monday and then it dropped by 2°C on Tuesday. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by 4°C. What was the temperature on this day?

Answer

Temperature on Monday= -5⁰C

Temperature on Tuesday = -5⁰C - 2⁰C = -7⁰C

Temperature on Wednesday= -7⁰C + 4⁰C = -3⁰C

Hence, the temperature on Tuesday and Wednesday was -7⁰C and -3⁰C.

4. A plane is flying at the height of 5000 m above the sea level. At a particular point, it is exactly above a submarine floating 1200 m below the sea level. What is the vertical distance between them?

Answer

Height of plane is above the sea level = 5000 m

A submarine is floating below the sea level = -1200m

Vertical distance between them = 5000 m - (-1200)m = 5000 m + 1200m = 6200m

5. Mohan deposits Rs 2,000 in his bank account and withdraws Rs 1,642 from it, the next day. If withdrawal of amount from the account is represented by a negative integer, then how will you represent the amount deposited? Find the balance in Mohan’s account after the withdrawal.

Answer

If withdrawal of amount from the account is represented by a negative integer, then the amount deposited will be represented by a positive integer.

A/q,

Amount deposited by Mohan = Rs. 2,000

Amount withdrawn = Rs. (-1642)

Balance in Mohan’s account = 2000 + (-1642) = 2000 - 1642 = 358

6. Rita goes 20 km towards east from a point A to the point B. From B, she moves 30 km towards west along the same road. If the distance towards east is represented by a positive integer then, how will you represent the distance travelled towards west? By which integer will you represent her final position from A?

Answer

If the distance towards east is represented by a positive integer then the distance travelled towards west will be represented by negative integer.

Distance travelled towards east direction = 20 km

Distance travelled towards west direction = 30 km

Distance travelled from A = 20 + (-30) = -10 km

7. In a magic square each row, column and diagonal have the same sum. Check which of the following is a magic square.

Answer

In square (i) each row, column and diagonal have the same sum i.e., 0. However, sum of one of its diagonals is not 0.

Therefore, square (i) is not a magic square.

In square (ii) each row, column and diagonal have the same sum i.e., -9.

Therefore, square (ii) is a magic square.

8. Verify a - (-b) = a + b for the following values of a and b.

(i) a = 21, b = 18

(ii) a = 118, b = 125

(iii) a = 75, b = 84

(iv) a = 28, b = 11

Answer

(i)a = 21, b= 18

→ a - (-b) = 21 - (-18) = 21 +18 = 39

→ a + b = 21 + 18 = 39

∴ a - (-b) = a + b = 39

(ii) a= 118, b= 125

→ a - (-b) = 118 - (-125) = 118 + 125 = 243

→ a + b = 118 + 125 = 243

∴ a - (-b) = a + b = 243

(iii)a=75, b= 84

→ a - (-b) = 75 - (-84) = 75 + 84 = 159

→ a + b = 75 + 84 = 159

∴ a - (-b) = a + b = 159

(iv)a=28, b= 11

→ a - (-b) = 28 - (-11) = 28 + 11 = 39

→ a + b = 28 +11 = 39

∴ a - (-b) = a + b = 39

9. Use the sign of >, < or = in the box to make the statements true.

(a) (–8) + (–4) ☐ (–8) – (–4)

(b) (–3) + 7 – (19) ☐ 15 – 8 + (–9)

(d) 39 + (–24) – (15)☐ 36 + (–52) – (–36)

(e) –231 + 79 + 51 ☐ –399 + 159 + 81

Answer

(a) LHS = (–8) + (–4) = -8-4 = -12

RHS = (–8) – (–4) = -8+4 = -4

∴ -12 < -4

(b) LHS = (–3) + 7 – (19) = -15

RHS = 15 – 8 + (–9) = 15 - 8 - 9 = -2

∴ -15 < -2

RHS = 23 – 41 – 11 = 29

∴ -7 > -29

(d) LHS = 39 + (-24) - (15) = 39 - 24 - 15 = 0

RHS = 36 + (-52) - (-36) = 36 - 52 + 36 = 20

∴ 0 < 20

(e) LHS = –231 + 79 + 51 = -101

RHS = –399 + 159 + 81 = -159

∴ -101 > -159

10. A water tank has steps inside it. A monkey is sitting on the topmost step (i.e., the first step). The water level is at the ninth step.

(i) He jumps 3 steps down and then jumps back 2 steps up. In how many jumps will he reach the water level?

(ii) After drinking water, he wants to go back. For this, he jumps 4 steps up and then jumps back 2 steps down in every move. In how many jumps will he reach back the top step?

(iii) If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers, represent his moves in part (i) and (ii) by completing the following; (a) – 3 + 2 – ... = – 8 (b) 4 – 2 + ... = 8. In (a) the sum (– 8) represents going down by eight steps. So, what will the sum 8 in (b) represent?

Answer

(a) The monkey was at step = 1

After first jump he will be at the step = 1+3 = 4

After second jump he will at the step = 4 + (-2) = 2

After third jump he will be at the step = 2 + 3 = 5

After fourth jump he will be at the step = 5 + (-2) = 3

After fifth jump he will be at the step = 3 + 3 = 6

After sixth jump he will be at the step = 6 + (-2) = 4

After seventh jump he will be at the step = 4 + 3 = 7

After eighth jump he will be at the step = 7 + (-2) = 5

After ninth jump he will be at the step = 5 + 3 = 8

After tenth jump he will at the step = 8 + (-2) = 6

After eleventh jump he will at the step = 6 + 3 = 9

Therefore, after 11th jump the monkey will reach the water level.

(b) The monkey was at the step 9.

After first jump he will be at the step = 9 + (-4) = 5

After second jump he will be at the step = 5 + 2 = 7

After third jump he will be at the step = 7 + (-4) = 3

After fourth jump he will be at the step = 3 + 2 = 5

After fifth jump he will be at the step = 5 + (-4) = 1

Therefore, after fifth jump he will reach back the top step.

(c) If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers, then his moves in part (i):

-3 + 2 -3 + 2 -3 + 2 -3 + 2 -3 + 2 -3 = -8

moves in part (ii):

4 -2 +4 -2 +4 = 8

Moves in part (ii) represent going up by 8 steps.

Page No: 8

Try these

1. Write a pair of integers whose sum gives

(a) a negative integer

(b) zero

(d) an integer smaller than only one of the integers.

(e) an integer greater than both the integers.

Answer

(a) 2 + (-8) = -6

(b) 4 + (-4) = 0
(c) -2 + -4 = -6
(d) 4 + (-2) = 2
(e) 2 + 5 = 7

2. Write a pair of integers whose difference gives

(a) a negative integer.

(b) zero.

(d) an integer greater than only one of the integers.

(e) an integer greater than both the integers.

Answer

(a) 2 - 8 = -6
(b) 4 - 4 = 0
(c) 2 - 7 = -5
(d) 9 - 3 = 6
(e) 4 - (-3) = 7

Page No: 9

Exercise 1.2

1. Write down a pair of integers whose:
(a) sum is -7
(b) difference is –10
(c) sum is 0

Answer

(a) -8 + (+1) = -7
(b) -12 – (-2) = -10
(c) 5 + (-5) = 0

2. (a) Write a pair of negative integers whose difference gives 8.
(b) Write a negative integer and a positive integer whose sum is –5.
(c) Write a negative integer and a positive integer whose difference is –3.

Answer

(a) -2 - (-10) = 8
(b) -8 +3 = -5
(c) -2 - (+1) = -3

3. In a quiz, team A scored – 40, 10, 0 and team B scored 10, 0, - 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?

Answer

Team A scored = -40, 10, 0

Total scored by Team A= -40 +10 +0 = -30

Team B scored = 10, 0, - 40

Total scored by Team B = 10 +0 + (-40) = -30

Hence, both teams scored equal.

4. Fill in the blanks to make the following statements true:

(i) (–5) + (............) = (– 8) + (............)

(ii) –53 + ............ = –53

(iii) 17 + ............ = 0

(iv) [13 + (– 12)] + (............) = ............ + [(–12) + (–7)]

(v) (– 4) + [............ + (–3)] = [............ + 15] + ............

Answer

(i) (-5) + (-8) = (-8) + (-5)

(ii) -53 + 0 = -53

(iii) 17 + (-17) = 0

(iv) [13 + (-12)] + (-7 ) = 13 + [(-12) + (-7)]

(v) (-4) + [15 + (-3)] = [-4 + 15] + (-3)

Page No: 10

Try these

Find:
4 × (– 8),
8 × (–2),
3 × (–7),
10 × (–1) using number line.

Answer

4 × (– 8) means -8 + (-8) + (-8) + 8) = -32

8 × (–2) means -2 + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) = -16

3 × (–7) means -7 + (-7) + (-7) = -21

10 × (–1) means -1 + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) = -10

Find:

(i) 6 × (-19)

(ii) 12 × (-32)

(iii) 7 × (-22)

Answer

(i) 6 × (-19) = -19 + (-19) + (-19) + (-19) + (-19) + (-19)= -114

(ii) 12 × (-32) = -32 + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) + (-32) = -144096

(iii) 7 × (-22) = -22 + (-22) + (-22) + (-22) + (-22) + (-22) + (-22)= -154

Page No. 11

Try these

1. Find:

(a) 15 × (–16)

(b) 21 × (–32)

(d) –55 × 15

Answer

(a) 15 × (–16) = 16 × (–15) = -240

(b) 21 × (–32) = 32 × (–21) = -672

(d) –55 × 15 = -825

2. Check if

(a) 25 × (–21) = (–25) × 21

(b) (–23) × 20 = 23 × (–20)

Write five more such examples.

Answer

(a) Yes.

25 × (–21) = (–25) × 21 = -525

(b) Yes.

(–23) × 20 = 23 × (–20) = -460

Five examples: (i) 15 × (–16) = 16 × (–15)

(ii) 14 × (–18) = 18 × (–14)

(iii) 25 × (–16) = 16 × (–25)

(iv) 28 × (–15) = 15 × (–28)

(v) 8 × (–16) = 16 × (–8)

Page No. 21

Exercise 1.3

1. Find each of the following products:

(a) 3 × (–1)

(b) (–1) × 225

(d) (–316) × (–1)

(e) (–15) × 0 × (–18)

(f) (–12) × (–11) × (10)

(g) 9 × (–3) × (– 6)

(h) (–18) × (–5) × (– 4)

(i) (–1) × (–2) × (–3) × 4

(j) (–3) × (–6) × (–2) × (–1)

Answer

(a) 3 x (–1) = –3

(b) (–1) x 225 = –225

(d) (–316) x (–1) = 316

(e) (–15) x 0 x (–18) = 0

(f) (–12) x (–11) x (10) = 132 x 10 = 1320

(g) 9 x (–3) x (–6) = 9 x 18 = 162

(h) (–18) x (–5) x (–4) = 90 x (–4) = –360

(i) (–1) x (–2) x (–3) x 4 = (–6 x 4) = –24

(j) (–3) x (–6) x (2) x (–1) = (–18) x (–2) = 36

2. Verify the following:

(a) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]

(b) (–21) × [(– 4) + (– 6)] = [(–21) × (– 4)] + [(–21) × (– 6)]

Answer

(a) 18 x [7 + (–3)] = [18 x 7] + [18 x (–3)]

⇒ 18 x 4 = 126 + (–54)

⇒ 72 = 72

⇒ L.H.S. = R.H.S. Hence verified.

(b) (–21) x [(–4) + (–6)] = [(–21) x (–4)] + [(–21) x (–6)]

⇒ (–21) x (–10) = 84 + 126

⇒ 210 = 210

⇒ L.H.S. = R.H.S. Hence verified.

3. (i) For any integer a, what is (–1) × a equal to?

(ii) Determine the integer whose product with (–1) is

(a) –22

(b) 37

Answer

(i) (–1)×a=–a, where aa is an integer.

(ii) (a) (–1)×(–22)=22

(b) (–1)×37=–37

4. Starting from (–1) × 5, write various products showing some pattern to show (–1) × (–1) = 1.

Answer

(–1)×5=–5(–1)×4=–4

(–1)×3=–3(–1)×2=–2

(–1)×1=–1(–1)×0=0

(–1)×(–1)=1

Thus, we can conclude that this pattern shows the product of one negative integer and one positive integer is negative integer whereas the product of two negative integers is a positive integer.

5. Find the product, using suitable properties:

(a) 26 × (– 48) + (– 48) × (–36)

(b) 8 × 53 × (–125)

(d) (– 41) × 102

(e) 625 × (–35) + (– 625) × 65

(f) 7 × (50 – 2)

(g) (–17) × (–29)

(h) (–57) × (–19) + 57

Answer

(a) 26×(–48)+(–48)×(–36)

⇒ (–48)×[26+(–36)] [Distributive property]

⇒ (–48)×(–10)

⇒ 480

(b) 8×53×(–125)

⇒ 53×[8×(–125)] [Commutative property]

⇒ 53×(–1000)

⇒ –53000

⇒ 15×[(–25)×(–4)×(–10)] [Commutative property]

⇒ 15×(–1000)

⇒ –15000

(d) (–41)×(102)

⇒ –41×[100+2] [Distributive property]

⇒ [(–41)×100]+[(–41)×2]

⇒ –4100+(–82)

⇒ –4182

(e) 625×(–35)+(–625)×65

⇒ 625×[(–35)+(–65)] [Distributive property]

⇒ 625×(–100)

⇒ –62500

(f) 7×(50–2)

⇒ 7×50–7×2 [Distributive property]

⇒ 350–14=336

(g) (–17)×(–29)

⇒ (–17)×[(–30)+1] [Distributive property]

⇒ (–17)×(30)+(–17)×1

⇒ 510+(–17)

⇒ 493

(h) (–57)×(–19)+57

⇒ (–57)×(–19)+57×1

⇒ 57 x 19 + 57 x 1

⇒ 57 x (19 + 1) [Distributive property]

⇒ 57 x 20 = 1140

6. A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5°C every hour. What will be the room temperature 10 hours after the process begins?

Answer

Given: Present room temperature = 40°C

Decreasing the temperature every hour = 5°C

Room temperature after 10 hours = 40°C + 10 x (–5°C)

= 40°C – 50°C

= –10°C

Thus, the room temperature after 10 hours is –10°C after the process begins.

7. In a class test containing 10 questions, 5 marks are awarded for every correct answer and (–2) marks are awarded for every incorrect answer and 0 for questions not attempted.

(i) Mohan gets four correct and six incorrect answers. What is his score?

(ii) Reshma gets five correct answers and five incorrect answers, what is her score?

(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?

Answer

(i) Mohan gets marks for four correct questions = 4 x 5 = 20

He gets marks for six incorrect questions = 6 x (–2) = –12

Therefore, total scores of Mohan = (4 x 5) + [6 x (–2)] = 20 – 12 = 8

Thus, Mohan gets 8 marks in a class test.

(ii) Reshma gets marks for five correct questions = 5 x 5 = 25

She gets marks for five incorrect questions = 5 x (–2) = –10

Therefore, total score of Resham = 25 + (–10) = 15

Thus, Reshma gets 15 marks in a class test.

(iii) Heena gets marks for two correct questions = 2 x 5 = 10

She gets marks for five incorrect questions = 5 x (–2) = –10

Therefore, total score of Resham = 10 + (–10) = 0

Thus, Reshma gets 0 marks in a class test.

8. A cement company earns a profit of Rs 8 per bag of white cement sold and a loss of Rs 5 per bag of grey cement sold.

(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?

(b) What is the number of white cement bags it must sell to have neither profit nor loss, if the number of grey bags sold is 6,400 bags.

Answer

Given: Profit of 1 bag of white cement = Rs. 8

And Loss of 1 bag of grey cement = Rs. 5

(a) Profit on selling 3000 bags of white cement = 3000 × 8 = Rs. 24,000

Loss of selling 5000 bags of grey cement = 5000 × Rs. 5 = Rs. 25,000

Since Profit < Loss

Therefore, his total loss on selling the grey cement bags = Loss – Profit

= 25,000 – 24,000 = Rs. 1,000

Thus, he has lost of Rs. 1,000 on selling the grey cement bags.

(b) Let the number of bags of white cement be x.

According to question, Loss = Profit

∴ 5 x 6,400 = x × 8

⇒ x = (5×6400)/8 = 5000 bags

Thus, he must sell 4000 white cement bags to have neither profit nor loss.

9. Replace the blank with an integer to make it a true statement.

(a) (–3) × _____ = 27

(b) 5 × _____ = –35

(d) _____ × (–12) = 132

Answer

(a) (−3)×(−9)−−−−=27

(b) 5×(−7)−−−−=−35

(d) (−11)−−−−−×(−12)=132

Page No. 26

Exercise 1.4

1. Evaluate each of the following:
(a) (−30)÷10
(b) 50÷(−5)
(c) (−36)÷(−9)
(d) (−49)÷49
(e) 13÷[(−2)+1]
(f) 0÷(−12)
(g) (−31)÷[(−30)+(−1)]
(h) [(−36)÷12]÷3
(i) [(−6)+5]÷[(−2)+1]

Answer

(a) (−30)÷10

= (−30)×1/10

= {(−30)×1}/10

= −3

(b) 50÷(−5)

= 50×(−1/5)

= {50×(−1)}/5

=−10

= (−36)×(−1/9)

= {(−36)×(−1)}/9

=36/9

(d) (−49)÷49

= (−49)× (1/49)

= −49/49

=−1

(e) 13÷[(−2)+1]

= 13÷(−1)

=13×(−1/1)

=−13

(f) 0÷(−12)

= 0×(−1/12)

=0/12

(g) (−31)÷[(−30)+(−1)]

= (−31)÷(−30−1)

=(−31)÷(−31)

=(−31)×(−1/31)

=31/31

(h) [(−36)÷12]÷3

= [(−36)×1/12]×1/3

=(−36/12)×1/3

=(−3)×1/3

=−3/3

=−1

(i) [(−6)+5]÷[(−2)+1]

= (−6+5)÷(−2+1)

=(−1)÷(−1)

=(−1)×(−1)/1

2. Verify that a÷(b+c) ≠ (a÷b)+(a÷c) for each of the following values of a,b and c.
(a) a=12,b=−4,c=2
(b) a=(−10),b=1,c=1

Answer
(a) Given: a÷(b+c) ≠ (a÷b)+(a÷c)
a=12,b=−4,c=2
Putting the given values in L.H.S. = 12÷(−4+2)
= 12÷(−2)

=12÷(−1/2)

= −12/2

=−6

Putting the given values in R.H.S. = [12÷(−4)]+(12÷2)

= (12×−14)+6

=−3+6

Since, L.H.S. ≠ R.H.S.
Hence, verified.

(b) Given: a÷(b+c) ≠ (a÷b)+(a÷c)
a=−10, b=1, c=1
Putting the given values in L.H.S. = −10÷(1+1)
= −10÷(2)

=−5

Putting the given values in R.H.S. = [−10÷1]+(−10÷1)

= −10−10

=−20

Since,
L.H.S. ≠ R.H.S.
Hence, verified.

3. Fill in the blanks:
(a) 369÷____=369
(b) (−75)÷____=(−1)
(c) (−206)÷____=1
(d) (−87)÷____=87
(e) ____÷1 = −87
(f) ____÷48 = −1
(g) 20÷ ___ = −2
(h) ___ ÷(4) = −3

Answer

(a) 369÷1 = 369

(b) (−75)÷75 = (−1)

(c) (−206)÷(−206) =1

(d) (−87)÷(−1) =87

(e) (−87) ÷1=−87

(f) (−48) ÷48=−1

(g) 20÷(−10) =−2

(h) (−12) ÷(4)=−3

4. Write five pairs of integers (a,b) such that a÷b = −3. One such pair is (6,−2) because 6÷(−2)=(−3).

Answer

(i) (−6)÷2=−3
(ii) 9÷(−3)=−3
(iii) 12÷(−4)=−3
(iv) (−9)÷3=−3
(v) (−15)÷5=−3

5. The temperature at noon was 10℃ above zero. If it decreases at the rate of 2℃ per hour until mid-night, at what time would the temperature be 8℃ below zero? What would be the temperature at mid-night?
Answer

Following number line is representing the temperature:

The temperature decreases 2°C = 1 hour
The temperature decreases 1°C = 1/2 hour
The temperature decreases 18°C = 1/2×18= 9 hours
Total time = 12 noon + 9 hours = 21 hours = 9 pm
Thus, at 9 pm the temperature would be 8oC below 0oC.

6. In a class test (+3) marks are given for every correct answer and (−2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores (−5) marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?
Answer

(i) Marks given for one correct answer = 3
Marks given for 12 correct answers = 3 x 12 = 36
Radhika scored 20 marks.
Therefore, Marks obtained for incorrect answers = 20 – 36 = –16
Now, marks given for one incorrect answer = –2
Therefore, number of incorrect answers = (−16)÷(−2) = 8(−16)÷(−2)=8
Thus, Radhika has attempted 8 incorrect questions.

(ii) Marks given for seven correct answers = 3 x 7 = 21
Mohini scores = –5
Marks obtained for incorrect answers = –5 –21 = –26
Now, marks given for one incorrect answer = –2
Therefore, number of incorrect answers = (−26) ÷ (−2) = 13
Thus, Mohini has attempted 13 incorrect questions.

7. An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 above the ground level, how long will it take to reach −350 m?
Answer

Starting position of mine shaft is 10 m above the ground but it moves in opposite direction so it travels the distance (–350) m below the ground.
So total distance covered by mine shaft = 10 m – (–350) m = 10 + 350 = 360 m
Now, time taken to cover a distance of 6 m by it = 1 minute
So, time taken to cover a distance of 1 m by it = 1/6 minute
Therefore, time taken to cover a distance of 360 m = 1/6×360 = 60 minutes = 1 hour
(Since 60 minutes = 1 hour)
Thus, in one hour the mine shaft reaches –350 below the ground.

Go To Chapters

↧

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.2

February 7, 2020, 1:31 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.3

≪ Previous: NCERT Solutions for Class 7th: Ch 1 Integers Math

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.2

If you are searching for NCERT Solutions of Chapter 14 Mathematical Reasoning Exercise 14.2 then you can find them here. NCERT Solutions of Class 11 Maths will cover all the basic details of the chapter so you can practice the questions and get all concept provided in the chapter. These will be helpful in boosting your marks in the examinations.

1. Write the negation of the given statements:

(i) Chennai is the capital of Tamil Nadu.

(ii) √2 is not a complex number.

(iii) All triangles are not equilateral triangle.

(iv) The number 2 is greater than 7.

(v) Every natural number is an integer.

Answer

(i) Chennai is not the capital of Tamil Nadu.

(ii) √2 is a complex number.

(iii) All triangles are equilateral triangles.

(iv) The number 2 is not greater than 7.

(v) Every natural number is not an integer.

2. Are the following pairs of statements negations of each other:

(i) The number x is not a rational number. The number x is not an irrational number.

(ii) The number x is a rational number. The number x is an irrational number.

Answer

(i) The negation of the first statement is “the number x is a rational number”. Which is the same as the second statement. This is because if that the number is not irrational, it is a rational. Therefore, the given pairs are negations of each other.

(ii) The negation of the first statement is “x is an irrational number” which is the same as the second statement. Therefore, the pairs are negations of each other.

3. Find the component statements of the following compound statements and check whether they are true or false.

(i) Number 3 is prime or it is odd.

(ii) All integers are positive or negative.

(iii) 100 is divisible by 3, 11 and 5.

Answer

(i) p: The number 3 is prime.
q: The number 3 is odd.
p, q are connected by or it is true.

(ii) p: All integers are positive.
q: All integers are negative.
p, q are connected by the word or p and q both are false.

(iii) p: 100 is divisible by 3
q: 100 is divisible by 11
q: 100 is divisible by 5
p is false, q is false, r is true
p and q and r is a false statement.

↧

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.3

February 7, 2020, 2:24 am

≫ Next: NCERT Solutions for Class 7th: Ch 2 Fractions and Decimals Geometry

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.2

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.3

Chapter 14 Mathematical Reasoning Exercise 14.3 NCERT Solutions is available here through which you can easily get solutions of every question. NCERT Solutions for Class 11 Maths is very helpful in knowing the concepts and important formula of the chapter. These NCERT Solutions are updated as per the latest pattern of CBSE.

1. For each of the following compound statements first identify the connecting words and then break it into component statements.

(i) All rational numbers are real and all real numbers are not complex.

(ii) Square of an integer is positive or negative.

(iii) The sand heats up quickly in the sun and does not cool down fast at night.

(iv) x = 2 and x = 3 are the roots of the equation 3x 2 – x – 10 = 0.

Answer

(i) “AND”
The component statements are:
All rational numbers are real.
All real numbers are not complex.

(ii) “OR”
The component statements are:
Square of an integer is positive.
Square of an integer is negative.

(iii) “AND”
The component statements are:
The sand heats up quickly in the sun.
The sand does not cool down fast at night.

(iv) “AND”
The component statements are:
x = 2 is a root of the equation 3x² – x – 10 = 0
x = 3 is a root of the equation 3x² – x – 10 = 0

2. Identify the quantifier in the given statements and write the negation of the statements.

(i) There exists a number which is equal to its square.

(ii) For every real number x, x is less than x + 1.

(iii) There exists a capital for every state in India.

Answer

(i) Quantifier is “there exists”.
Negation is: There does not exist a number which is equal to its square.

(ii) Quantifier: For every p: for every real number x, x is less than x + 1.
~ p: There exist a real number x such that x is not less than x + 1.

(iii) Quantifier is: “There exists”.
The negation statement is: There exists a state in India which does not have a capital.

3. Check whether the following pair of statements are negation of each other. Give reasons for your answer.

(i) x + y = y + x is true for every real numbers x and y.

(ii) There exists real numbers x and y for which x + y = y + x.

Answer

Statement (i) and (ii) are not the negation of each other.

4. State whether the "OR" used in the following statements is "exclusive or inclusive". Give reasons for your answer.

(i) Sun rises or Moon sets.

(ii) To apply for a driving licence, you should have a ration card or a passport.

(iii) All integers are positive or negative.

Answer

(i) When sun rise the moon sets. One of the happenings will take place. Here 'OR' is exclusive

(ii) To apply for a driving licence either a ration card or a passport or both can be used.
∴ "OR" used here is inclusive.

(iii) All integers are positive or negative. An integer cannot be both + ve and – ve at time.
∴ Here "OR" is exclusive.

↧

NCERT Solutions for Class 7th: Ch 2 Fractions and Decimals Geometry

February 7, 2020, 4:31 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.4

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.3

NCERT Solutions for Chapter 2 Fractions and Decimals Class 7 Mathematics

Page No: 31

Exercise 2.1

1. Solve:
(i) 2 - 3/5
(ii) 4 + 7/8
(iii) 3/5 + 2/7
(iv) 9/11 − 4/15
(v) 7/10 + 2/5 + 3/2
(vi) 2⅔ + 3½
(vii) 8½ − 3⅝

Answer

(i) 2−3/5 = (10−3)/5 = 7/5
(ii) 4+7/8 = (32+7)/8 = 39/8
(iii) 3/5 + 2/7 = (21+10)/35 = 31/35
(iv) 9/11 − 4/15 = (135−44)/165 = 91/165
(v) 7/10 + 2/5 + 3/2 = (7+4+15)/10 = 26/10 = 13/5
(vi) 2⅔ + 3½ = 8/3 + 7/2 = (16+21)/6 = 37/6 = 6.1/6
(vii) 8½ − 3⅝ = 17/2−29/8 = (68−29)/8 = 39/8 = 4.7/8

2. Arrange the following in descending order:
(i) 2/9,2/3,8/21
(ii) 1/5,3/7,7/10

Answer

(i) 2/9,2/3,8/21
⇒ 14/63,42/63,24/63 [Converting into like fractions]
⇒ 42/63>24/63>14/63 [Arranging in descending order]
Therefore, 2/3>8/21>2/9

(ii) 1/5,3/7,7/10 ⇒14/70,30/70,49/70 [Converting into like fractions]
⇒ 49/70>30/70>14/70 [Arranging in descending order]
Therefore, 7/10>3/7>1/5

3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?

(Along the first row 4/11+9/11+2/11=15/11)(Along the first row 4/11+9/11+2/11=15/11)

Answer

Sum of first row = 4/11+9/11+2/11=15/11 [Given]
Sum of second row = 3/11+5/11+7/11=(3+5+7)/11=15/11
Sum of third row = 8/11+1/11+6/11=(8+1+6)/11=15/11
Sum of first column = 4/11+3/11+8/11=(4+3+8)/11=15/11
Sum of second column = 9/11+5/11+1/11=(9+5+1)/11=15/11
Sum of third column = 2/11+7/11+6/11=(2+7+6)/11=15/11
Sum of first diagonal (left to right) = 4/11+5/11+6/11=(4+5+6)/11=15/11
Sum of second diagonal (left to right) = 2/11+5/11+8/11=(2+5+8)/11=15/11
Since, the sum of fractions in each row, in each column and along the diagonals are same, therefore, it s a magic square.

4. A rectangular sheet of paper is 12½ cm long and 10⅔ cm wide. Find its perimeter.

Answer

The sheet of paper is in rectangular form.
Length of sheet = 12½ cm and Breadth of sheet = 10⅔ cm
Perimeter of rectangle = 2 (length + breadth)
= 2(12½ +10⅔) = 2(25/2+32/3)
= 2{(25×3+32×2)/6} = 2{(75+64)/6}
= 2×139/6 = 139/3 = 46.(1/3) cm.
Thus, the perimeter of the rectangular sheet is 46.1/3 cm.

5. Find the perimeter of (i) ΔABE, (ii) the rectangle BCDE in this figure. Whose perimeter is greater?

Answer

(i) In ΔABE, AB = 5/2 cm, BE = 2.(3/4) cm, AE = 3.(3/5) cm
The perimeter of ΔABE = AB + BE + AE
= 5/2 + 2.(3/4) + 3.(3/5) = 5/2 + 11/4 + 18/5
= (50+55+72)/20 = 177/20 = 8.(17/20) cm
Thus, the perimeter of ΔABE is 8.(17/20) cm.

(ii) In rectangle BCDE, BE = 2.3/4 cm, ED = 7/6 cm
Perimeter of rectangle = 2 (length + breadth)
= 2(2.3/4+7/6) = 2(11/4+7/6)
= 2{(33+14)/12} = 47/6 = 7.(5/6) cm
Thus, the perimeter of rectangle BCDE is 7.(5/6) cm.
Comparing the perimeter of triangle and that of rectangle,
8.17/20 cm > 7.5/6 cm
Therefore, the perimeter of triangle ABE is greater than that of rectangle BCDE.

6. Salil wants to put a picture in a frame. The picture is 7.(3/5) cm wide. To fit in the frame the picture cannot be more than 7.3/10 cm wide. How much should the picture be trimmed?

Answer

Given: The width of the picture = 7.(3/5) cm and the width of picture frame = 7.(3/10) cm
Therefore, the picture should be trimmed = 7.(3/5) − 7.(3/10) = 38/5 = 73/10
= (76−73)/10 = 3/10 cm
Thus, the picture should be trimmed by 3/10 cm.

7. Ritu ate 3/5 part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?

Answer

The part of an apple eaten by Ritu = 3/5
The part of an apple eaten by Somu = 1−3/5 = (5−3)/5 = 2/5
Comparing the parts of apple eaten by both Ritu and Somu 3/5 > 2/5
Larger share will be more by 3/5−2/5 = 1/5 part.
Thus, Ritu’s part is 1/5 more than Somu’s part.

8. Michael finished colouring a picture in 7/12 hour. Vaibhav finished colouring the same picture in 3/4 hour. Who worked longer? By what fraction was it longer?

Answer

Time taken by Michael to colour the picture = 7/12 hour
Time taken by Vaibhav to colour the picture = 3/4 hour
Converting both fractions in like fractions, 7/12 and (3×3)/(4×3)=9/12
Here, 7/12 < 9/12 ⇒ 7/12<3/4
Thus, Vaibhav worked longer time.
Vaibhav worked longer time by 3/4−7/12=(9−7)/12=2/12=1/6 hour.
Thus, Vaibhav took 1/6 hour more than Michael.

Page No. 36

Exercise 2.2

1. Which of the drawings (a) to (d) show:

(i) 2×1/5

(ii) 2×1/2

(iii) 3×2/3

(iv) 3×1/4

(a)

(b)

(c)

(d)

Answer

(i) – (d) Since 2×1/5=1/5+1/5

(ii) – (b) Since 2×1/2=1/2+1/2

(iii) – (a) Since 3×2/3=2/3+2/3+2/3

(iv) – (c) Since 3×1/4=1/4+1/4+1/4

2. Some pictures (a) to (c) are given below. Tell which of them show:

(i) 3×1/5 = 3/5

(ii) 2×1/3 = 2/3

(iii) 3×3/4 = 2.(1/4)

Answer

(i) – (c) Since 3×1/5=1/5+1/5+1/5

(ii) – (a) Since 2×1/3=1/3+1/3

(iii) – (b) Since 3×3/4=3/4+3/4+3/4

3. Multiply and reduce to lowest form and convert into a mixed fraction:

(i) 7 × 3/5

(ii) 4 × 1/3

(iii) 2 × 6/7

(iv) 5 × 2/9

(v) 2/3 × 4

(vi) 5/2 × 6

(vii) 11 × 4/7

(viii) 20 × 4/5

(ix) 13 × 1/3

(x) 15 × 3/5

Answer

(i) 7× 3/5
= (7×3)/5
= 21/5
=4.(1/5)

(ii) 4× 1/3
= (4×1)/3
= 4/3
=1.(1/3)

(iii) 2× 6/7
= (2×6)/7
= 12/7
=1.(5/7)

(iv) 5× 2/9
= (5×2)/9
= 10/9
=1.(1/9)

(v) 2/3 × 4
= (2×4)/3
= 8/3
= 2.(2/3)

(vi) 5/2 × 6
= 5×3
= 15

(vii) 11× 4/7
= (11×4)/7
= 44/7
= 6.(2/7)

(viii) 20× 4/5
= 4×4
= 16

(ix) 13× 1/3
= (13×1)/3
= 13/3
=4.(1/3)

(x) 15× 3/5
= 3×3
= 9

4. Shade:

(i) 2/3 of the triangles in box (a)

(ii) 3/5 of the squares in box (b)

(i) 1/2 of the circles in box (c)

Answer

(i) 2/3 of 9 triangles = 2/3 ×9 = 2×3 = 6 triangles

(ii) 3/5 of 15 squares = 3/5 ×15 = 3 × 3 = 9 squares

(iii) 1/2 of 12 circles = 1/2 ×12 = 6 circles

5. Find:

(a) 1/2 of (i) 24 (ii) 46

(b) 2/3 of (i) 18 (ii) 27

(d) 4/5 of (i) 20 (ii) 35

Answer

(a)

(i) 1/2 of 24 = 12

(ii) 1/2 of 46 = 23

(b)

(i) 2/3 of 18 = 2/3×18 = 2 × 6 = 12

(ii) 2/3 of 27 = 2/3×27 = 2 × 9 = 18

(c)

(i) 3/4 of 16 = 3/4 × 16 = 3 × 4 = 12

(ii) 3/4 of 36 = 3/4 × 36 = 3 × 9 = 27

(d)

(i) 4/5 of 20 = 4/5 × 20 = 4 × 4 = 16

(ii) 4/5 of 35 = 4/5 × 35 = 4 × 7 = 28

6. Multiply and express as a mixed fraction:

(a) 3× 5.(1/5)

(b) 5× 6.(3/4)

(d) 4× 6.(1/3)

(e) 3.(1/4) ×6

(f) 3.(2/5) ×8

Answer

(a) 3× 5.1/5
= 3× 26/5
= (3×26)/5
= 78/5
= 15.(3/5)

(b) 5× 6.(3/4)
= 5× 27/4
= (5×27)/4
= 135/4
= 33.(3/4)

(d) 4×6.1/3
= 4× 19/3
= (4×19)/3
= 76/3
= 25.1/3

(e) 3.(1/4) ×6
= 13/4 ×6
= (13×3)/2
= 39/2
= 19.(1/2)

(f) 3.2/5×8
= 17/5 ×8
= (17×8)/5
= 136/5
= 27.(1/5)

7. Find:

(a) 1/2 of (i) 2.(3/4) (ii) 4.(2/9)

(b) 5/8 of (i) 3.(5/6) (ii) 9.(2/3)

Answer

(a)

(i) 1/2 of 2.(3/4) = 1/2×11/4 = 11/8 = 1.(3/8)

(ii) 1/2 of 4.(2/9) = 1/2 × 38/9 = 19/9 = 2.(1/9)

(b)

(i) 5/8 of 3.(5/6) = 5/8 × 23/6 = 115/48 = 2.(19/48)

(ii) 5/8 of 9.(2/3) = 5/8 × 29/3 = 145/24 = 6.(1/24)

8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed 2/5 of the water. Pratap consumed the remaining water.

(i) How much water did Vidya drink?

(ii) What fraction of the total quantity of water did Pratap drink?

Answer

Total quantity of water in bottle = 5 litres

(i) Vidya consumed = 2/5 of 5 litres = 2/5×5 = 2 litres

Thus, Vidya drank 2 litres water from the bottle.

(ii) Pratap consumed = (1−2/5) part of bottle = 5−2/5=3/5 part of bottle

Pratap consumed 3/5 of 5 litres water = 3/5×5 = 3 litres

Thus, Pratap drank 3/5 part of the total quantity of water.

Page No. 41

Exercise 2.3

1. Find:

(i) 1/4 of

(a) 1/4

(b) 3/4

(ii)1/7 of

(a) 2/9

(b) 6/5

Answer

(i) (a) 1/4 of 1/4
= 1/4×1/4
=(1×1)/(4×4)
=1/16

(b) 1/4 of 3/4
= 1/4×3/4
=(1×3)/(4×4)
= 3/16

(ii) (a) 1/7 of 2/9
= 1/7×2/9
=(1×2)/(7×9)
=2/63

(b) 1/7 of 2/9
= 1/7×6/5
=(1×6)/(7×5)
=6/35

(i) 2/3 × 2.(2/3)

(ii) 2/7 × 7/9

(iii) 3/8 × 6/4

(iv) 9/5 × 3/5

(v) 1/3 × 15/8

(vi) 11/2 × 3/10

(vii) 4/5 × 12/7

Answer

(i) 2/3 × 2.2/3
= 2/3 × 8/3
= (2×8)/(3×3)
= 16/9
= 1.(7/9)

(ii) 2/7 × 7/9
= (2×7)/(7×9)
= 2/9

(iii) 3/8 × 6/4
= (3×6)/(8×4)
= (3×3)/(8×2)
= 9/16

(iv) 9/5 × 3/5
= (9×3)/(5×5)
= 27/25
= 1.(2/25)

(v) 1/3 × 15/8
= (1×15)/(3×8)
= (1×5)/(1×8)
= 5/8

(vi) 11/2 × 3/10
=(11×3)/(2×10)
=33/20
=1.(3/20)

(vii) 4/5 × 12/7
=(4×12)/(5×7)
=48/35
=1.(13/35)

3. Multiply the following fractions:

(i) 2/5 × 5.(1/4)

(ii) 6.(2/5) × 7/9

(iii) 3/2 × 5.(1/3)

(iv) 5/6 × 2.(3/7)

(v) 3.(2/5) × 4/7

(vi) 2.(3/5) × 3

(vii) 3.(4/7) × 3/5

Answer

(i) 2/5 × 5.(1/4)
= 2/5 × 21/4
= (2×21)/(5×4)
= (1×21)/(5×2)
= 21/10
= 2.(1/10)

(ii) 6.(2/5) × 7/9
= 32/5 × 7/9
= (32×7)/(5×9)
= 224/45
= 4.(44/45)

(iii) 3/2×5.(1/3)
= 3/2 × 16/3
= 48/6
= 8

(iv) 5/6×2.(3/7)
= 5/6 × 17/7
= 85/42
= 2.(1/42)

(v) 3.(2/5) × 4/7
= 17/7 × 4/7
= 68/35
= 1.(33/35)

(vi) 2.(3/5) × 3
= 13/5 × 3/1
= (13×3)/(5×1)
= 39/5
= 7.(4/5)

(vii) 3.(4/7) × 3/5
= 25/7 × 3/5
= (5×3)/(7×1)
= 15/7
= 2.(1/7)

4. Which is greater:

(i) 2/7 of 3/4 or 3/5 of 5/8

(ii) 1/2 of 6/7 or 2/3 of 3/7

Answer

(i) 2/7 of 3/4 or 3/5 of 5/8
⇒ 2/7 × 3/4 or 3/5 × 5/8

⇒ 3/14 or 3/8
⇒ 3/14<3/8

Thus, 3/5 of 5/8 is greater.

(ii) 1/2 of 6/7 or 2/3 of 3/7
⇒ 1/2 × 6/7 or 2/3 × 3/7

⇒ 3/7 or 2/7
⇒ 3/7 > 2/7

Thus, 1/2 of 6/7 is greater.

5. Saili plants 4 saplings in a row in her garden. The distance between two adjacent saplings is 3/4 m. Find the distance between the first and the last sapling.

Answer

The distance between two adjacent saplings = 3/4 m

Saili planted 4 saplings in a row, then number of gap in saplings

Therefore, the distance between the first and the last saplings = 3×3/4 = 9/4m = 2.(1/4) m

Thus the distance between the first and the last saplings is 2.(1/4) m.

6. Lipika reads a book for 1.3/4 hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?

Answer

Time taken by Lipika to read a book = 1.(3/4) hours.

She reads entire book in 6 days.

Now, total hours taken by her to read the entire book = 1.3/4×6 = 7/4×6=21/2=10.1/2 hours

Thus, 10 hours were required by her to read the book.

7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using 2.3/4 litres of petrol?

Answer

In 1 litre of pertrol, car covers the distance = 16 km

In 2.3/4 litres of petrol, car covers the distance = 2.3/4 of 16 km = 11/4×16 = 44 km

Thus, car will cover 44 km distance.

8. (a) (i) Provide the number in the box ___ , such that 2/3× ___ = 10/30

(ii) The simplest form of the number obtained in ___ is _____.

(b) (i) Provide the number in the box ____ such that 3/5× ____ = 24/75

(ii) The simplest form of the number obtained in ___ is ____.

Answer

(a) (i) 2/3×5/10=10/30

(ii) The simplest form of 5/10 is 1/2

(b) (i) 3/5×8/15=24/75

(ii) The simplest form of 8/15 is 8/15

Page No. 46

Exercise 2.4

1. Find:
(i) 12 ÷ 3/4
(ii) 14 ÷ 5/6
(iii) 8 ÷ 7/3
(iv) 4 ÷ 8/3
(v) 3 ÷ 2.(1/3)
(vi) 5 ÷ 3.(4/7)

Answer

(i) 12÷3/4 = 12 × 4/3 = 16
(ii) 14 ÷ 5/6 = 14 × 6/5 = 84/5 = 16.(4/5)
(iii) 8 ÷ 7/3 = 8× 3/7 = 24/7 = 3.(3/7)
(iv) 4÷ 8/3 = 4× 3/8 = 3/2 = 1.(1/2)
(v) 3÷ 2.(1/3) = 3÷ 7/3 = 3× 3/7 = 9/7 = 1.(2/7)
(vi) 5÷ 3.(4/7) = 5÷ 25/7 = 5× 7/25 = 7/5 = 1.(2/5)

2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fraction, improper fractions and whole numbers.
(i) 3/7
(ii) 5/8
(iii) 9/7
(iv) 6/5
(v) 12/7
(vi) 1/8
(vii) 1/11

Answer

(i) Reciprocal of 3/7 = 7/3 → Improper fraction
(ii) Reciprocal of 5/8 = 8/5 → Improper fraction
(iii) Reciprocal of 9/7 = 7/9 → Proper fraction
(iv) Reciprocal of 6/5 = 5/6 →Proper fraction
(v)Reciprocal of 12/7 = 7/12 → Proper fraction
(vi) Reciprocal of 1/8 = 8 → Whole number
(vi) Reciprocal of 1/11 = 11 → Whole number

3. Find:
(i) 7/3 ÷2
(ii) 4/9 ÷5
(iii) 6/13 ÷7
(iv) 4.(1/3) ÷3
(v) 3.(1/2) ÷4
(vi) 4.(3/7) ÷7

Answer

(i) 7/3 ÷ 2 = 7/3 × ½ = (7×1)/(3×2) = 7/6 = 1.(1/6)
(ii) 4/9 ÷ 5 = 4/9 × 1/5 = (4×1)/(9×5) = 4/45
(iii) 6/13 ÷ 7 = 6/13 × 1/7 = (6×1)/(13×7) = 6/91
(iv) 4.(1/3) ÷ 3 = 13/3 ÷ 3 = 13/3 × 1/3 = 13/9 = 1.(4/9)
(v) 3.(1/2) ÷ 4 = 7/2 ÷ 4 = 7/2 × ¼ = 7/8
(vi) 4.(3/7) ÷ 7 = 31/7 ÷ 7 = 31/7 × 1/7 = 31/49

4. Find:
(i) 2/5 ÷ 1/2
(ii) 4/9 ÷ 2/3
(iii) 3/7 ÷ 8/7
(iv) 2.1/3 ÷ 3/5
(v) 3.1/2 ÷ 8/3
(vi) 2/5 ÷ 1.1/2
(vii) 3.1/5 ÷ 1.2/3
(viii) 2.1/5÷1.1/5

Answer

(i) 2/5 ÷ ½
= 2/5 × 2/1 = (2×2)/(5×1) =4/5

(ii) 4/9 ÷ 2/3
= 4/9 × 3/2 = 2/3

(iii) 3/7 ÷ 8/7
= 3/7 × 7/8 = 3/8

(iv) 2.(1/3) ÷ 3/5
= 7/3 ÷ 3/5 = 7/3 × 5/3 = 35/9 = 3.(8/9)

(v) 3.(1/2) ÷ 8/3
= 7/2 ÷ 8/3 = 7/2 × 3/8 = (7×3)/(2×8) = 21/16 = 1.(5/16)

(vi) 2/5 ÷ 1.(1/2)
= 2/5 ÷ 3/2 = 2/5 × 2/3 = (2×2)/(5×3) = 4/15

(vii) 3.(1/5) ÷ 1.(2/3)
= 16/5 ÷ 5/3 = 16/5 × 3/5 = (16×3)/(5×5) = 48/25 = 1.(23/25)

(viii) 2.(1/5) ÷ 1.(1/5)
= 11/5 ÷ 6/5 = 11/5 × 5/6 = 11/6 = 1.(5/6)

Page No. 47

Exercise 2.5

1. Which is greater:

(i) 0.5 or 0.05

(ii) 0.7 or 0.5

(iii) 7 or 0.7

(iv) 1.37 or 1.49

(v) 2.03 or 2.30

(vi) 0.8 or 0.88

Answer

(i) 0.50 > 0.05

(ii) 0.7 > 0.5

(iii) 7.0 > 0.7

(iv) 1.37 < 1.49

(v) 2.03 < 2.30

(vi) 0.80 < 0.88

2. Express as rupees using decimals:

(i) 7 paise

(ii) 7 rupees 7 paise

(iii) 77 rupees 77 paise

(iv) 50 paise

(v) 235 paise

Answer

∵ 100 paise = Re. 1

∴ 1 paisa = Re. 1/100

7 paise = Re. 7/100 = Re. 0.07

7 rupees 7 paise = Rs. 7 + Re. 7/100 = Rs. 7 + Re. 0.07 = Rs. 7.07

77 rupees 77 paise = Rs. 77 + Re. 77/100 = Rs. 77 + Re. 0.77 = Rs. 77.77

50 paise = Re. 50/100 = Re. 0.50

235 paise = Re. 235/100 = Rs. 2.35

3. (i) Express 5 cm in metre and kilometer.

(ii) Express 35 mm in cm, m and km.

Answer

(i) Express 5 cm in meter and kilometer.

∵ 100 cm = 1 meter

∴ 1 cm = 1/100 meter ⇒ 5 cm = 5/100 = 0.05 meter.

Now, ∵ 1000 meters = 1 kilometers

∴ 1 meter = 1/1000 kilometer

⇒ 0.05 meter = 0.05/1000 = 0.00005 kilometer

(ii) Express 35 mm in cm, m and km.

∵ 10 mm = 1 cm

∴ 1 mm = 1/10 cm ⇒ 35 mm = 35/10 = 3.5 cm

Now, ∵ 100 cm = 1 meter

∴ 1 cm = 1/100 meter ⇒3.5 cm = 3.5/100 = 0.035 meter

Again, ∵ 1000 meters = 1 kilometers

∴ 1 meter = 1/1000 kilometer

⇒ 0.035 meter = 0.035/1000 = 0.000035 kilometer

4. Express in kg.:

(i) 200 g

(ii) 3470 g

(iii)4 kg 8 g

Answer

1000 g = 1 kg ⇒ 1 g = 1/1000 kg

(i) 200 g = (200× 1/1000) kg = 0.2 kg

(ii) 3470 g = (3470× 1/1000) kg = 3.470 kg

(iii) 4 kg 8 g = 4 kg + (8× 1/1000) kg = 4 kg + 0.008 kg = 4.008 kg

5. Write the following decimal numbers in the expanded form:

(i) 20.03

(ii) 2.03

(iii) 200.03

(iv) 2.034

Answer

(i) 20.03 = 2×10 + 0×1 + 0×1/10 + 3×1/100

(ii) 2.03 = 2×1+0×1/10+3×1/100

(iii) 200.03 = 2×100+0×10+0×1+0×1/10+3×1/100

(iv) 2.034 = 2×1+0×1/10+3×1/100+4×1/1000

6. Write the place value of 2 in the following decimal numbers:

(i) 2.56

(ii) 21.37

(iii) 10.25

(iv) 9.42

(v) 63.352

Answer

(i) Place value of 2 in 2.56 = 2 × 1 = 2 ones

(ii) Place value of 2 in 21.37 = 2 × 10 = 2 tens

(iii) Place value of 2 in 10.25 = 2× 1/10 = 2 tenths

(iv) Place value of 2 in 9.42 = 2× 1/100 = 2 hundredth

(v) Place value of 2 in 63.352 = 2× 1/1000 = 2 thousandth

7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?

Answer

Distance travelled by Dinesh when he went from place A to place B = 7.5 km and from place B to C = 12.7 km.

Total distance covered by Dinesh = AB + BC

= 7.5 + 12.7 = 20.2 km

Total distance covered by Ayub = AD + DC

= 9.3 + 11.8 = 21.1 km

On comparing the total distance of Ayub and Dinesh,

21.1 km > 20.2 km

Therefore, Ayub covered more distance by 21.1 – 20.2 = 0.9 km = 900 m

8. Shyam bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?

Answer

Total weight of fruits bought by Shyam = 5 kg 300 g + 3 kg 250 g = 8 kg 550 g

Total weight of fruits bought by Sarala = 4 kg 800 g + 4 kg 150 g = 8 kg 950 g

On comparing the quantity of fruits,

8 kg 550 g < 8 kg 950 g

Therefore, Sarala bought more fruits.

9. How much less is 28 km than 42.6 km?

Answer

We have to find the difference of 42.6 km and 28 km.

42.6 – 28.0 = 14.6 km

Therefore 14.6 km less is 28 km than 42.6 km

Page No. 52

Exercise 2.6

1. Find:

(i) 0.2 × 6

(ii) 8 × 4.6

(iii) 2.71 × 5

(iv) 20.1 × 4

(v) 0.05 × 7

(vi) 211.02 × 4

(vii) 2 × 0.86

Answer

(i) 0.2 × 6 = 1.2

(ii) 8 × 4.6 = 36.8

(iii) 2.71 × 5 = 13.55

(iv) 20.1 × 4 = 80.4

(v) 0.05 × 7 = 0.35

(vi) 211.02 × 4 = 844.08

(vii) 2 × 0.86 = 1.72

2. Find the area of rectangle whose length is 5.7 cm and breadth is 3 cm ?

Answer

Given: Length of rectangle = 5.7 cm and Breadth of rectangle = 3 cm

Area of rectangle = Length × Breadth

= 5.7 × 3 = 17.1 cm²

Thus, the area of rectangle is 17.1 cm²

3. Find:

(i) 1.3 × 10

(ii) 36.8 × 10

(iii) 153.7 × 10

(iv) 168.07 × 10

(v) 31.1 × 100

(vi) 156.1 × 100

(vii) 3.62 × 100

(viii) 3.07 × 100

(ix) 0.5 × 10

(x) 0.08 × 10

(xi) 0.9 × 100

(xii) 0.03 × 1000

Answer

(i) 1.3 × 10 = 13.0

(ii) 36.8 × 10 = 368.0

(iii) 153.7 × 10 = 1537.0

(iv) 168.07 × 10 = 1680.7

(v) 31.1 × 100 = 3110.0

(vi) 156.1 × 100 = 15610.0

(vii) 3.62 × 100 = 362.0

(viii) 43.07 × 100 = 4307.0

(ix) 0.5 × 10 = 5.0

(x) 0.08 × 10 = 0.80

(xi) 0.9 × 100 = 90.0

(xii) 0.03 × 1000 = 30.0

4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?

Answer

∵ In one litre, a two-wheeler covers a distance = 55.3 km

∴ In 10 litrs, a two- wheeler covers a distance = 55.3 × 10 = 553.0 km

Thus, 553 km distance will be covered by it in 10 litres of petrol.

5. Find:

(i) 2.5 × 0.3

(ii) 0.1 × 51.7

(iii) 0.2 × 316.8

(iv) 1.3 × 3.1

(v) 0.5 × 0.05

(vi) 11.2 × 0.15

(vii) 1.07 × 0.02

(viii) 10.05 × 1.05

(ix) 101.01 × 0.01

(x) 100.01 × 1.1

Answer

(i) 2.5 × 0.3 = 0.75

(ii) 0.1 × 51.7 = 5.17

(iii) 0.2 × 316.8 = 63.36

(iv) 1.3 × 3.1 = 4.03

(v) 0.5 × 0.05 = 0.025

(vi) 11.2 × 0.15 = 1.680

(vii) 1.07 × 0.02 = 0.0214

(viii) 10.05 × 1.05 = 10.5525

(ix) 101.01 × 0.01 = 1.0101

(x) 100.01 × 1.1 = 110.11

Page No. 55

Exercise 2.7

1. Find:
(i) 0.4 ÷ 2
(ii) 0.35 ÷ 5
(iii) 2.48 ÷ 4
(iv) 65.4 ÷ 6
(v) 651.2 ÷ 4
(v) 14.49 ÷ 7
(vii) 3.96 ÷ 4
(viii) 0.80 ÷ 5

Answer

(i) 0.4 ÷ 2
= 4/10 × 1/ 2= 2/10 = 0.2

(ii) 0.35 ÷ 5
= 35/100 × 1/5 = 7/100 = 0.07

(iii)2.48 ÷ 4
= 248/100 × 1/4 = 62/100 = 0.62

(iv) 65.4 ÷ 6
= 654/10 × 1/6 = 109/10 = 10.9

(v) 651.2 ÷ 4
= 6512/10 × 1/4 = 1628/10 = 162.8

(vi) 14.49 ÷ 7
= 1449/100 × 1/7 = 207/100 = 2.07

(vii) 3.96 ÷ 4
= 396/100 × 1/4 = 99/100 = 0.99

(viii) 0.80 ÷ 5
= 80/100 × 1/5 = 16/100 = 0.16

2. Find:
(i) 4.8 ÷ 10
(ii) 52.5 ÷ 10
(iii) 0.7 ÷ 10
(iv) 33.1 ÷ 10
(v) 272.23 ÷ 10
(vi) 0.56 ÷ 10
(vii) 3.97 ÷ 10

Answer

(i) 4.8 ÷ 10
= 4.8/10 = 0.48

(ii) 52.5 ÷ 10
= 52.5/10 = 5.25

(iii) 0.7 ÷ 10
= 0.7/10 = 0.07

(iv) 33.1 ÷ 10
= 33.1/10 = 3.31

(v) 272.23 ÷ 10
= 272.23/10 = 27.223

(vi) 0.56 ÷ 10
= 0.56/10 = 0.056

(vii) 3.97 ÷ 10
= 3.97/10 = 0.397

3. Find:
(i) 2.7 ÷ 100
(ii) 0.3 ÷ 100
(iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100
(v) 23.6 ÷ 100
(vi) 98.53 ÷ 100

(i) 2.7 ÷ 100
= 27/10 × 1/100 = 27/1000 = 0.027

(ii) 0.3 ÷ 100
= 3/10 × 1/100 =3/1000 = 0.003

(iii) 0.78 ÷ 100
= 78/100 × 1/100 = 78/10000 = 0.0078

(iv) 432.6 ÷ 100
= 4326/10 × 1/100 = 4326/1000 = 4.326

(v) 23.6 ÷ 100
= 236/10 × 1/100 = 236/1000 = 0.236

(vi) 98.53 ÷ 100
= 9853/100 × 1/100 = 9853/10000 = 0.9853

4. Find:
(i) 7.9 ÷ 1000
(ii) 26.3 ÷ 1000
(iii) 38.53 ÷ 1000
(iv) 128.9 ÷ 1000
(v) 0.5 ÷ 1000

Answer

(i) 7.9 ÷ 1000
= 79/10 × 1/1000 = 79/10000 = 0.0079

(ii) 26.3 ÷ 1000
= 263/10 × 1/1000 = 263/10000 = 0.0263

(iii) 38.53 ÷ 1000
= 3853/100 × 1/1000 = 3853/100000 = 0.03853

(iv) 128.9 ÷ 1000
= 1289/10 × 1/1000 = 1289/10000 = 0.1289

(v) 0.5 ÷ 1000
= 5/10 × 1/1000 = 5/10000 = 0.0005

5. Find:
(i) 7 ÷ 3.5
(ii) 36 ÷ 0.2
(iii) 3.25 ÷ 0.5
(iv) 30.94 ÷ 0.7
(v) 0.5 ÷ 0.25
(vi) 7.75 ÷ 0.25
(vii) 76.5 ÷ 0.15
(viii) 37.8 ÷ 1.4
(ix) 2.73 ÷ 1.3

Answer

(i) 7 ÷ 3.5
= 7 ÷ 35/10 = 7 × 10/35 = 10/5 = 2

(ii) 36 ÷ 0.2
= 36 ÷ 2/10 = 36 × 10/2 = 18 × 10 = 180

(iii) 3.25 ÷ 0.5
= 325/100 ÷ 5/10 = 325/100 × 10/5 = 65/10 = 6.5

(iv) 30.94 ÷ 0.7
= 3094/100 ÷ 7/10 = 3094/100 × 10/7 = 442/10 = 44.2

(v) 0.5 ÷ 0.25
= 5/10 ÷ 25/100 = 5/10 × 100/25 = 10/5 = 2

(vi) 7.75 ÷ 0.25
= 775/100 ÷ 25/100 = 775/100 × 100/25 = 31

(vii) 76.5 ÷ 0.15
= 765/10 ÷ 15/100 = 765/10 × 100/15 = 51×10 = 510

(viii) 37.8 ÷ 1.4
= 378/10 ÷ 14/10 = 378/10 × 10/14 = 27

(ix) 2.73 ÷ 1.3
= 273/100 ÷ 13/10 = 273/100 × 10/13 = 21/10 = 2.1

6. A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre petrol?

Answer

∵ In 2.4 litres of petrol, distance covered by the vehicle = 43.2 km
∴ In 1 litre of petrol, distance covered by the vehicle = 43.2 ÷ 2.4
= 432/10 ÷ 24/10 = 432/10 × 10/24
= 18 km
Thus, it covered 18 km distance in one litre of petrol.

Go to Chapters list

↧

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.4

February 7, 2020, 8:04 am

≫ Next: NCERT Solutions for Class 7th: Ch 3 Data Handling Geometry

≪ Previous: NCERT Solutions for Class 7th: Ch 2 Fractions and Decimals Geometry

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.4

Chapter 14 Mathematical Reasoning Exercise 14.4 Class 11 Maths NCERT Solutions is given here that are accurate so you can check your answers with these and boost your marks in the examinations. Practicing NCERT Solutions for Class 11 Maths will give you details how to apply important fomula and knowing the basic points of the chapter.

1. Rewrite the following statement with “if-then” in five different ways conveying the same meaning.

‘If a natural number is odd, then its square is also odd.’

Answer

(i) A natural number is odd implies that its square is odd.

(ii) The natural number is odd only if its square is odd.

(iii) If the square of a natural number is not odd then the natural number is also not odd.

(iv) For a natural number to be odd it is necessary that its square is odd.

(v) For a square of a natural number to be odd, it is sufficient that the number is odd.

2. Write the contrapositive and converse of the following statements:

(i) If x is a prime number, then x is odd.

(ii) If the two lines are parallel, then they do not intersect in the same plane.

(iii) Something is cold implies that it has low temperature.

(iv) You cannot comprehend geometry if you do not know how to reason deductively.

(v) x is an even number implies that x is divisible by 4.

Answer

(i) Given statement: If x is a prime number, then x is odd.

The contrapositive statement: If a number x is not odd, then x is not a prime number.

The converse statement: If a number x is odd, then it is a prime number.

(ii) Given statement: If the two lines are parallel, then they do not intersect in the same plane.

The contrapositive statement: If two lines intersect in the same plane, then they are not parallel.

The converse statement: If two lines do not intersect in the same plane, then they are parallel.

(iii) Given statement: Something is cold implies that it has low temperature.

The contrapositive statement: If something is not at low temperature, then it is not cold.

The converse statement: If something is at low temperature, then it is cold.

(iv) Given statement: You cannot comprehend geometry if you do not know how to reason deductively.

The contrapositive statement: If you know how to reason deductively, then you cannot comprehend geometry.

The converse statement: If you do not know how to reason deductively, then you cannot comprehend geometry.

(v) Given statement: x is an even number implies that x is divisible by 4.

It can be written as: “If x is an even number, then x is divisible by 4”.

The contrapositive statement: If x is not divisible by 4, then x is not an even number.

The converse statement: If x is divisble by 4, then x is an even number.

3. Write each of the following statements in the form ‘if-then’.

(i) “You get a job implies that your credentials are good”.

(ii) The Banana trees will bloom if it stays warm for a month.

(iii) A quadrilateral is a parallelogram if its diagonals bisect each other.

(iv) To get an A+ in the class, it is necessary that you do all the exercise of the book.

Answer

(i) If you get a job then your credentials are good.

(ii) If it stays warm for a month the Banana trees will bloom.

(iii) If diagonals of a quadrilateral bisect each other then it is a parallelogram.

(iv) If you get an A+ in the class then you do all the exercises of the book.

4. Given statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.

(a) If you live in Delhi, then you have winter clothes.

(i) If you do not have winter clothes, then you do not live in Delhi.

(ii) If you have winter clothes, then you live in Delhi

(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.

(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.

(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

Answer

(a) (i) Contrapositive statement.

(ii) Converse statement.

(b) (i) Contrapositive statement.

(ii) Converse statement.

↧

NCERT Solutions for Class 7th: Ch 3 Data Handling Geometry

February 7, 2020, 9:24 am

≫ Next: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.5

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.4

NCERT Solutions for Chapter 3 Data Handling Class 7 Mathematics

Page No: 62

Exercise 3.1

1. Find the range of heights of any ten students of your class.

Answer

S. No.	Name of students	Height (in feet)
1	Gunjan	4.2
2	Aditi	4.5
3	Nikhil	5
4	Akhi	5.1
5	Riya	5.2
6	Akshat	5.3
7	Abhishek	5.1
8	Mayank	4.7
9	Rahul	4.9
10	Ayush	4.5

Range = Highest height – Lowest height = 5.3 – 4.2 = 1.1 feet

2. Organize the following marks in a class assessment, in a tabular form:
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7.
(i) Which number is the highest?
(ii) Which number of the lowest?
(iii) What is the range of the lowest?
(iv) Find the arithmetic mean.

Answer

S. No.	Marks	Tally marks	Frequency (No. of students)
1 2 3 4 5 6 7 8 9	1 2 3 4 5 6 7 8 9		1 2 1 5 4 2 1 1

Please arrange the tally marks image in table.
(i) The highest number is 9.
(ii) The lowest number is 1.
(iii) The range of the data is 9 – 1 = 8
(iv) Arithmetic mean = 4+6+7+5+3+5+4+5+2+6+2+5+1+9+6+5+8+4+6+7/20 = 100/20 = 5

3. Find the mean of the first five whole numbers.

Answer

The first five whole numbers are 0, 1, 2, 3 and 4.
Therefore, Mean of first five whole numbers = Sum of numbers/Total number
= (0+1+2+3+4)/5 = 10/5 = 2
Thus, the mean of first five whole numbers is 5.

4. A cricketer scores the following runs in eight innings: 58, 76, 40, 35, 46, 45, 0, 100. Find the mean score.

Answer

Number of innings = 8
Mean of score = (Sum of scores)/(Number of innings)
= (58+76+40+35+46+45+0+100)/8
Thus, the mean score is 50.

5. Following table shows the points of each player scored in four games:

Player	Game 1	Game 2	Game 3	Game 4
A	14	16	10	10
B	0	8	6	4
C	8	11	Did not play	13

Now answer the following questions:
(i) Find the mean to determine A’s average number of points scored per game.
(ii) To find the mean number of points per game for C, would you divide the total points by 3 or 47? Why?
(iii) B played in all the four games. How would you find the mean?
(iv) Who is the best performer?

Answer

(i) Mean of player A = (Sum of scores by A)/(No. of games played by A)
= (14+16+10+10)/4=50/4 = 12.5

(ii) We should divide the total points by 3 because player C played only three games.

(iii) Player B played in all the four games.
∴ Mean of player B = (Sum of scores by B)/(No. of games played by B)
= (0+8+6+4)/4=18/4 = 4.5

(iv) To find the best performer, we should know the mean of all players.
Mean of player A = 12.5
Mean of player B = 4.5
Mean of player C = (8+11+13)/3=32/3 = 10.67
Therefore, on comparing means of all players, player A is the best performer.

6. The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the:
(i) The highest and the lowest marks obtained by the students.
(ii) Range of the marks obtained.
(iii) Mean marks obtained by the group.

Answer

(i) Highest marks obtained by the student = 95
Lowest marks obtained by the student = 39

(ii) Range of marks = Highest marks – Lowest marks
= 95 – 39 = 56

(iii) Mean of obtained marks = (Sum of marks)/(Total number of marks)
= (85+76+90+85+39+48+56+95+81+75)/10
= 730/10 = 73
Thus, mean marks obtained by the group of students is 73.

7. The enrolment in a school during six consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2820. Find the mean enrolment of the school for this period.

Answer

Mean enrolment = (Sum of numbers of enrolment)/(Total number of years)
= (1555+1670+1750+2013+2540+2820)/6 = 12348/6 = 2058
Thus, the mean enrolment of the school is 2,058.

8. The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:

Day	Mon	Tue	Wed	Thru	Fri	Sat	Sun
Rainfall (in mm)	0	12.2	2.1	0	20.5	5.5	1

(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfall?

Answer

(i) The range of the rainfall = Highest rainfall – Lowest rainfall
= 20.5 – 0.0 = 20.5 mm

(ii) Main rainfall = (Sum of rainfall recorded)/(Total number of days)
= (0.0+12.2+2.1+2.2+20.5+5.5+1.0)/7
= 41.37 = 5.9 mm

(iii) 5 days. i.e., Monday, Wednesday, Thursday, Saturday and Sunday rainfalls were less than the mean rainfall.

9. The height of 10 girls were measured in cm and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
(i) What is the height of the tallest girl?
(ii) What is the height of the shortest girl?
(iii) What is the range of data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height?

Answer

(i) The height of the tallest girl = 151 cm

(ii) The height of the shortest girl = 128 cm

(iii) The range of the data = Highest height – Lowest height
= 151 – 128 = 23 cm

(iv) The mean height = (Sum of heights of the girls)/(Total numebr of girls)
= (135+150+139+128+151+132+146+149+143+141)/10
= 1414/10 = 141.4 cm

(v) Five girls, i.e., 150, 151, 146, 149, 143 have heights (in cm) more than the mean height.

Page No. 68

Exercise 3.2

1. The scores in mathematics test (out of 25) of students is as follows:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
Find the mode and median of this data. Are they same?

Answer

Arranging the given data in ascending order,
5, 9, 10, 12, 15, 16, 19, 20, 20, 20, 20, 23, 24, 25, 25
Mode is the observation occurred the highest number of times.
Therefore, Mode = 20
Median is the middle observation = 20
Yes, Mode and Median are same of given observation.

2. The runs scored in a cricket match by 11 players is as follows:
6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 15
Find the mean, mode and median of this data. Are the three same?

Answer

Arranging the given data in ascending order,
6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120
Mean = (Sum of observations)/(Number of observations)
= (6+8+10+10+15+15+15+50+80+100+120)/11 = 429/11 = 39
Mode is the observation occurred the highest number of times = 15
Median is the middle observation = 15
Therefore, Mode and Median is 15.
No, the mean, median and mode are not same.

3. The weight (in kg) of 15 students of a class are:
38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47
(i) Find the mode and median of this data.
(ii) Is there more than one mode?

Answer

Arranging the given data in ascending order,
32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43, 43, 45, 47, 50
(i) Mode is the observation occurred the highest number of times.
Therefore, Mode = 38 and 43
(ii) Median is the middle observation = 40
Yes, there are 2 modes.

4. Find the mode and median of the data:
13, 16, 12, 14, 19, 12, 14, 13, 14

Answer

Arranging the given data in ascending order,
12, 12, 13, 13, 14, 14, 14, 16, 19
Mode is the observation occurred the highest number of times = 14
Median is the middle observation = 14

5. Tell whether the statement is true or false:
(i) The mode is always one of the numbers in a data.
(ii) The mean is one of the numbers in a data.
(iii) The median is always one of the numbers in a data.
(iv) The data 6, 4, 3, 8, 9, 12, 13, 9 has mean 9.

Answer

(i) True
(ii) False
(iii) True
(iv) False

Page No. 72

Exercise 3.3

1. Use the bar graph to answer the following questions:
(a) Which is the most popular pet?
(b) How many students have dog as a pet?

Answer

(a) Cat is the most popular pet.
(b) 8 students have dog as a pet.

2. Read the bar graph which shows the number of books sold by a bookstore during five consecutive years and answer the following questions:
(i) About how many books were sold in 1989? 1990? 1992?
(ii) In which year were about 475 books sold? About 225 books sold?
(iii) In which years were fewer than 250 books sold?
(iv) Can you explain how you would estimate the number of books sold in 1989?

Answer

According to the given bar graph,
(i) In 1989, 180 books were sold.
In 1990, 475 books were sold.
In 1992, 225 books were sold.
(ii) In 1990, about 475 books were sold and in 1992, about 225 books were sold.
(iii) In 1989 and 1992 fewer than 250 books were sold.
(iv) By reading the graph, we calculate that 180 books were sold in 1989.

3. Number of children in six different classes are given below. Represent the data on a bar graph.

Class	Fifth	Sixth	Seventh	Eighth	Ninth	Tenth
No. of children	135	120	95	100	90	80

(b) Answer the following questions:
(i) Which class has the maximum number of children? And the minimum?
(ii) Find the ratio of students of class sixth to the students of class eighth.

Answer

Data represented by the bar graph is as follows:
(a) Scale: 1 unit = 25 children

(b) (i) Fifth class has the maximum number of children and Tenth class has the minimum number of children.
(ii) Ratio = (Number of students in class sixth)/(Number of students in class eighth) = 120/100 = 6/5 = 6 : 5

4. The performance of a student in 1st term and 2nd term is given. Draw a double bar graph choosing appropriate scale and answer the following:

Subject	English	Hindi	Maths	Science	S. Science
1st term (MM. 100)	67	72	88	81	73
2nd term (MM (100)	70	65	95	85	75

(i) In which subject has the child improved his performance the most?
(ii) In which subject is the improvement the least?
(iii) Has the performance gone down in any subject?

Answer

Data represented by bar graph is as follows:
Difference of marks of 1st term and 2nd term
English = 70 – 67 = 3, Hindi = 65 – 72 = -7, Maths = 95 – 88 = 7, Science = 85 – 81 = 4, S. Science = 75 – 73 = 2
(i) He has most improved in Maths subject.
(ii) In S. Science subject, his improvement is less.
(iii) Yes, in Hindi subject, his performance has gone down.

5. Consider this data collected from a survey of a colony.

Favourite Sport	Cricket	Basket Ball	Swimming	Hockey	Athletics
Watching	1240	470	510	423	250
Participating	620	320	320	250	105

(i) Draw a double bar graph choosing an appropriate scale. What do you infer from the bar graph?
(ii) Which sport is most popular?
(iii) Which is more preferred, watching or participating in sports?

Answer

Data represented by the double bar graph is as follows:
(i)This bar graph represents the number of persons who are watching and participating in their favourite sports.
(ii) Cricket is most popular.
(iii) Watching sports is more preferred.

6. Take the data giving the minimum and the maximum temperature of various cities given in the beginning of this Chapter. Plot a double bar graph using the data and answer the following:
Temperature of Cities as on 20.6.2006

City	Ahmedabad	Amritsar	Bangalore	Chennai
Max.	38 ̊C	37 ̊C	28 °C	36 °C
Min.	29 ̊C	26 ̊C	21 °C	27 C
City	Delhi	Jaipur	Jammu	Mumbai
Max.	38 ̊C	39 ̊C	41 °C	32 °C
Min.	29 ̊C	29 ̊C	26 °C	27 °C

(i) Which city has the largest difference in the minimum and maximum temperature on the given data?
(ii) Which is the hottest city and which is the coldest city?
(iii) Name two cities where maximum temperature of one was less than the minimum temperature of the order.
(iv) Name the city which has the least difference between its minimum and the maximum temperature.

Answer

Data represented by double bar graph is as follows:
(i) Jammu has the largest difference in temperature i.e., Maximum temperature = 41 ̊C and Minimum temperature =26 ̊C
∴ Difference = 41 ̊C − 26 ̊C = 15 ̊
(ii) Jammu is the hottest city due to maximum temperature is high and Bangalore is the coldest city due to maximum temperature is low.
(iii) Maximum temperature of Bangalore = 28 ̊C
Minimum temperature of two cities whose minimum temperature is higher than the maximum temperature of Bangalore are Ahemedabad and Jaipur = 29 ̊C
(iv) Mumbai has the least difference in temperature i.e., Maximum temperature = 32 ̊C and Minimum temperature = 27 ̊C
∴ Difference = 32 ̊C − 27 ̊C = 5 ̊C

Page No. 76

Exercise 3.4

Tell whether the following is certain to happen, impossible can happen but not certain.
(i) You are older today than yesterday.
(ii) A tossed coin will land heads up.
(iii) A die when tossed shall land up with 8 on top.
(iv) The next traffic light seen will be green.
(v) Tomorrow will be a cloudy day.

Answer

(i) It is certain to happen.
(ii) It can happen but not certain.
(iii) It is impossible.
(iv) It can happen but not certain.
(v) It can happen but not certain.

2. There are 6 marbles in a box with numbers from 1 to 6 marked on each of them.
(i) What is the probability of drawing a marble with number 2?
(ii) What is the probability of drawing a marble with number 5?

Answer

Total marbles from 1 to 6 marked in a box = 6
(i) The probability of drawing a marble with number 2.
⇒ P (drawing one marble) = 1/6
(ii) The probability of drawing a marble with number 5.
⇒ P (drawing one marble) = 1/6

3. A coin is flipped to decide which team starts the game. What is the probability that your team will start?

Answer

A coin has two possible outcomes Head and Tail.
Probability of getting Head or Tail is equal.
∴ P (Starting game) = 1/2

Go to Chapters list

↧

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.5

February 8, 2020, 1:20 am

≫ Next: NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

≪ Previous: NCERT Solutions for Class 7th: Ch 3 Data Handling Geometry

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.5

Chapter 14 Mathematical Reasoning Exercise 14.5 Class 11 Maths NCERT Solutions are very useful if you want to improve your problem solving skills. Here, you will find NCERT Solutions for Class 11 Maths which are prepared by Studyrankers expert that will help you in completing your homework. By practicing NCERT Questions, you will get to know about important points provided in the chapter.

1. Show that the statement p:
"If x is real number such that x³ + 4x = 0 then x = 0" is true by
(i) Direct method
(ii) Method of contradiction
(iii) Method of contrapositive.

Answer

(i) Direct method.
x³ + 4x = 0 or x(x² + 4) = 0
=> x² + 4 ≠ 0, x ∈ R hence, x = 0
(ii) Method of contradiction.
Let x ≠ 0 and let it be x = p, p∈ R, p is a root of x³ + 4x = 0
∴ p³ + 4p = 0 ∴ p(p2 + 4) = 0
p ≠ 0 Also p² + 4 0 => p = 0
(iii) Contrapositive. q is not true
=> Let x = 0 is not true
=> let x = p ≠ 0 ∴ p³+ 4p = 0,
p being the root of x ² + 4 = 0
or p(p² + 4) = 0, Now, p = 0 Also p² + 4 ≠ 0 => p(p ² + 4) ≠ 0 if p is not true
∴ x = 0 is the root of x³ + 4x = 0.

2. Show that the statement “For any real numbers a and b, a² = b² implies that a = b” is not true by giving a counter-example.

Answer

Let a = 1, b = –1
and a² = b² but a ≠ b
Thus we observe that the given statement is not true.

3. Show that the following statement is true by the method of contrapositive.
p: If x is an integer and x² is even then x is also even.

Answer

Let x is not even -i.e. x = 2n + 1
∴ x² = (2n + 1)² = 4n² + 4n + 1
= 4(n² + n) + 1
4(x² + x) + 1 is odd. i.e. "If q is not true then p is not true" is proved
Hence, the given statement is true.

4. By giving counter example, show that the following statements are not true.
(i) p: If all the angles of a triangle are equal, then the triangle is an obtuse angled triangle.
(ii) q: The equation x² – 1 = 0 does not have a root lying between 0 and 2.

Answer

(i) Let an angle of triangle be 90 + θ
∴ Sum of the angles = 3(90 + θ)
= 270 + 3θ which is greater than 180°
A triangle having equal angles cannot be obtuse angle triangle.

(ii) The equation x² – 1 = 0 has the root x = 1 which lies between 0 and 2.
Then, given statement is not ture.

5. Which of the following statements are true and which are false? In each case give a valid reason for saying so.

(i) p: Each radius of a circle is a chord of the circle.

(ii) q: The centre of a circle bisects each chord of the circle.

(iii) r: Circle is a particular case of an ellipse.

(iv) s: If x and y are integers such that x > y, then –x < –y.

(v) t: √11 is a rational number.

Answer

(i) False: The end points of radius do not lie on the circle. Therefore, it is not a chord.
(ii) False: Only diameters are bisected at the centre. Other chords do not pass through the centre. Therefore centre cannot bisect them.
(iii) True: Equation of ellipse is x²/a² + y²/b² = 1
When b = a, the equation becomes x²/a² + y²/a² or x² + y ² = a² which is the equation of the circle.
(iv) True: If x and y are integers and x > y then – x < – y. By rule of inequality.
(v) False: 11 is prime number.
∴ √11 is irrational.

↧

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

February 8, 2020, 8:28 am

≫ Next: NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2

≪ Previous: NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.5

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

You can find Chapter 3 Coordinate Geometry Exercise 3.1 Class 9 Maths NCERT Solutions here. You will find accurate solutions of every questions of the exercise that will build your fundamentals. These will come handy in completing your homework and will boost your morale. NCERT Solutions for Class 9 Maths are prepared by Studyrankers experts and will guide you how to apply formula correctly so you can go for advance maths books. It will also prepare you for higher classes and entrance exams.

There are only two questions in the exercise 3.1 in which you have to describe the position of a table lamp on your study table to another person?

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

↧

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2

February 8, 2020, 9:25 am

≫ Next: NCERT Solutions for Class 10 Ch 1 Power Sharing Civics

≪ Previous: NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2

Want to access NCERT solutions of Chapter 3 Coordinate Geometry Exercise 3.2 then you can easily get them here. Class 9 Maths NCERT Solutions can help you in ascertaining answers of difficult questions easily so you can complete your homework easily. These NCERT answers are updated as per the latest marking scheme released by CBSE.

Exercise 3.2 has only two questions in which you have to name horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane, What is the name of each part of the plane formed by these two lines etc.

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2 Part 1

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2 Part 2

↧

NCERT Solutions for Class 10 Ch 1 Power Sharing Civics

February 9, 2020, 3:22 am

≫ Next: NCERT Solutions for Class 10 Ch 2 Federalism Civics

≪ Previous: NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2

NCERT Solutions for Class 10 Ch 1 Power Sharing Civics Social Studies (S.St)

Chapter 1 Power Sharing NCERT Solutions for Class 10 Civics will be useful in knowing the useful points given in the chapter. This chapter contains many important topics such as accommodation in Belgium, majoritarianism in Sri Lanka, why power sharing is desirable, forms of power-sharing such as among different organs of government, among governments at different levels, among different social groups and among political parties, pressure groups and movements. NCERT Solutions for Ch 1 Power Sharing will help you in revising these topics in better manner.

NCERT Solutions for Class 10th: Ch 1 Power Sharing Civics

Study Reference for Class 10 Chapter 1 Power Sharing
Revision Notes for Chapter 1 Power Sharing Extra Questions for Chapter 1 Power Sharing Class 10 MCQs Test of Chapter 1 Power Sharing Video for Chapter 1 Power Sharing Part-I Video for Chapter 1 Power Sharing Part-II

Study Reference for Class 10 Chapter 1 Power Sharing

In Text Questions

Page No: 2

1. I have a simple equation in mind. Sharing power = dividing power = weakening the country. Why do we start by talking of this?

Answer

Sharing of power does not always mean weakening the country. Sometimes, it may create the problem by delaying decisions which are for the welfare of the people but many times it creates the possibilities of better decision making.

→ It ensures that people coming from different spheres have 'say' in the government.

→ It also ensures that maximum people can participate in the government making decision more democratic.

→ It also helps in reducing conflict between different social groups hence, make country more powerful.

Page No: 4

1. What’s wrong if the majority community rules? If Sinhalas don’t rule in Sri Lanka, where else will they rule?

Answer

Ruling by the majority does not mean oppression of the minority. Sinhalas which are in majority and in government in Sri Lanka disregarding the wishes and needs of the minority. In modern era, oppression is not morally correct to be in power. Democracy works on the majority of opinion, not by major community. A democratically elected government must be sensible to the people's demands and protect citizen's basic rights.

Page No. 9

1. In my school, the class monitor changes every month. Is that what you call a power sharing arrangement?

Answer

This is not power sharing arrangement as the class monitor has all the power at a time and this power is shifted to another in next month. There is no check on his/her power. The power must be shared among others which is an important feature of power sharing.

Page No: 10

Exercises

1. What are the different forms of power sharing in modern democracies? Give an example of each of these.

Answer

The different forms of power sharing in modern democracies are:

→ Horizontal Distribution of Power: The power is shared among the different organs of government, such as the legislature, executive and judiciary. Example: The distribution of power between Indian Parliament (legislature), the council of ministers headed by chief ministers (executive) and Courts of India.

→ Vertical Distribution of Power: The power is shared among governments at different levels– a general government for the entire country and governments at the provincial or regional level. Example: In India, power is shared among Central government, State government and local governments.

→ Distribution of Power among different Social Groups: Power may also be shared among different social groups such as the religious and linguistic groups.Example: ‘Community Government’ in Belgium.

→ Distribution of Power among Political Parties, Pressure Groups and Movements: Political Parties, Pressure Groups and Movements control or influence those who are in power. Different political parties contest elections for power which ensures that power does not remain in one hand and shared among different political parties that represent different ideologies and social groups. Pressure groups and movements influence the decision making process.

2. State one prudential reason and one moral reason for power sharing with an example from the Indian context.

Answer

→ Prudential Reason: Power sharing helps in reducing the conflict between various social groups. Hence, power sharing is necessary for maintaining social harmony and peace. In India, seats are reserved for the weaker sections of society. Example: reservation of seats for scheduled castes and scheduled tribes. This allows the weaker sections also to participate in the running of the Government.

→ Moral Reason: It upholds the spirit of democracy. In a truly democratic setup, the citizens too have a stake in governance. In India, the citizens can come together to debate and criticise the policies and decisions of the government. This in turn puts pressure on the government to rethink its policies and reconsider its decisions.

3. After reading this chapter, three students drew different conclusions. Which of these do you agree with and why? Give your reasons in about 50 words.
Thomman - Power sharing is necessary only in societies which have religious, linguistic or ethnic divisions.
Mathayi - Power sharing is suitable only for big countries that have regional divisons.
Ouseph - Every society needs some form of power sharing even if it is small or does not have social divisions.

Answer

Ouseph's statement is the most logical, and thus, should be agreed on. Every society needs some form of power sharing even if it is small or does not have social divisions. A democratic society is one where its members or citizens through participation acquire a stake in the system. Power sharing not only prevents conflict between various groups in the society but it also generates a sense of belongingness among them to the society. Power sharing helps to maintain a balance of power among various institutions and also keep a check on how it is exercised. Irrespective of the size of a country or the type of a society, people will be more satisfied where they have a say in the functioning and decision making processes of the system.

4. The Mayor of Mrchtem, a town near Brussels in Belgium, has defended a ban on speaking French in the town’s schools. He said that a ban would help all non-Dutch speakers integrate in this Flemish town. Do you think that this measure is in keeping with the spirit of Belgium’s power sharing arrangements? Give your reasons in about 50 words.

Answer

No, This measure is not in keeping with Belgium's power sharing arrangements. The arrangements seek to maintain peace between the French and Dutch-speaking communities. By banning French, the mayor will cause civil unrest. Both the languages should be made acceptable in the town's schools. This bilingual education system will be a better way to integrate the people of the town.

Page No: 5

5. Read the following passage and pick out any one of the prudential reasons for power sharing offered in this.
"We need to give more power to the panchayats to realise the dream of Mahatma Gandhi and the hopes of the makers of our Constitution. Panchayati Raj establishes true democracy. It restores power to the only place where power belongs in a democracy - in the hands of the people. Given power to panchayats is also a way to reduce corruption and increase administrative efficiency. When people participate in the planning and implementation of developmental schemes, they would naturally exercise greater control over these schemes. This would eliminate the corrupt middlemen. Thus, Panchayati Raj will strengthen the foundations of our democracy."

Answer

The prudential reason for power sharing offered in this passage is giving power to panchayats is also a way to reduce corruption and increase administrative efficiency.

6. Different arguments are usually put forth in favour of and against power sharing. Identify those which are in favour of power sharing and select the answer using the codes given below? Power sharing:
A. reduces conflict among different communities
B. decreases the possibility of arbitrariness
C. delays decision making process
D. accommodates diversities
E. increases instability and divisiveness
F. promotes people's participation in government
G. undermines the unity of a country

(a)	A	B	D	F
(b)	A	C	E	F
(c)	A	B	D	G
(d)	B	C	D	G

Answer

(a)

7. Consider the following statements about power sharing arrangements in Belgium and Sri Lanka.
A. In Belgium, the Dutch-speaking majority people tried to impose their domination on the minority French-speaking community.
B. In Sri Lanka, the policies of the government sought to ensure the dominance of the Sinhala-speaking majority.
C. The Tamils in Sri Lanka demanded a federal arrangement of power sharing to protect their culture, language and equality of opportunity in education and jobs.
D. The transformation of Belgium from unitary government to a federal one prevented a possible division of the country on linguistic lines.
Which of the statements given above are correct?
(a) A, B, C and D
(b) A, B and D
(c) C and D
(d) B, C and D

Answer

(d) B, C and D

Page No: 12

8. Match list I (forms of power sharing) with List II (forms of government) and select the correct answer using the codes given below in the lists:

	List I		List II
1.	Power shared among different organs of government	Α.	Community government
2.	Power shared among governments at different levels	Β.	Separation of powers
3.	Power shared by different social groups	C.	Coalition government
4.	Power shared by two or more political parties	D.	Federal government

	1	2	3	4
(a)	D	A	B	C
(b)	B	C	D	A
(c)	B	D	A	C
(d)	C	D	A	B

Answer

	1	2	3	4
(c)	B	D	A	C

9. Consider the following two statements on power sharing and select the answer using the codes given below:
A. Power sharing is good for democracy.
B. It helps to reduce the possibility of conflict between social groups.
Which of these statements are true and false?

(a)A is true but B is false

(b) Both A and B are true

(c) Both A and B are false

(d)A is false but B is true

Answer

(b) Both A and B are true

Go Back To NCERT Solutions for Class 10 Civics

↧

NCERT Solutions for Class 10 Ch 2 Federalism Civics

February 9, 2020, 3:22 am

≫ Next: NCERT Solutions for Class 10th Science: Ch 1 Chemical Reactions and Equations

≪ Previous: NCERT Solutions for Class 10 Ch 1 Power Sharing Civics

NCERT Solutions for Class 10 Ch 2 Federalism Civics Social Studies (S.St)

NCERT Solutions for Class 10 Civics Ch 2 Federalism will help you in revising the topics of the chapter such as what is federalism, features of federalism, kinds of federation, what makes India a federal country, linguistic states, language policy, center state relations, decentralisation in India and many others. Chapter 2 Federalism NCERT Solutions Social Science will help you in completing your homework as these are prepared by subject matter experts.

Study Reference for Class 10 Chapter 2 Federalism
Revision Notes for Chapter 2 Federalism Extra Questions for Chapter 2 Federalism Class 10 MCQs Test of Chapter 2 Federalism

Study Reference for Class 10 Chapter 2 Federalism

Page No: 27

Exercises

1. Locate the following States on a blank outline political map of India:
Manipur, Sikkim, Chhattisgarh and Goa

Answer

2. Identify and shade three federal countries (other than India) on a blank outline political map of the world.

Answer

3. Point out one feature in the practice of federalism in India that is similar to and one feature that is different from that of Belgium.

Answer

In India, just like in Belgium, the central government has to share its powers with the regional governments. However, unlike India, Belgium has a community government in addition to the central and the state government.

4. What is the main difference between a federal form of government and a unitary one? Explain with an example.

Answer

In a federal form of government, the central government shares its powers with the various constituent units of the country. For example, in India, power is divided between the government at the Centre and the various State governments.
In a unitary form of government, all the power is exercised by only one government. For example, in Sri Lanka, the national government has all the powers.

5. State any two differences between the local government before and after the constitutional amendment in 1992.

Answer

Local governments Before 1992	Local governments After 1992
Elections were controlled by the state and not held regularly.	An independent State Election Commissionis responsible to conduct elections regularly.
Local governments did not have any powers or resources of their own.	The State governments are required to share some powers and revenue with local government bodies.

6. Fill in the blanks:
Since the United States is a ____________________ type of federation, all the constituent States have equal powers and States are _______________ vis-à-vis the federal government. But India is a _________________ type of federation and some States have more power than others. In India, the ___________________ government has more powers.

Answer

Since the United States is a coming together type of federation, all the constituent States have equal powers and States are strong vis-à-vis the federal government. But India is a holding together type of federation and some States have more power than others. In India, the Central government has more powers.

7. Here are three reactions to the language policy followed in India. Give an argument and an example to support any of these positions.
Sangeeta: The policy of accommodation has strengthened national unity.
Arman: Language-based States have divided us by making everyone conscious of their language.
Harish: This policy has only helped to consolidate the dominance of English over all other languages.

Answer

I agree with Sangeeta's reaction. If the policy of accommodation was not followed, and states were not created on linguistic basis, there would have been further partition of India. For example, imposition of Hindi as the national language would have led the South to break away from the North and Tamil Nadu would have become an independent nation.

8. The distinguishing feature of a federal government is:
(a) National government gives some powers to the provincial governments.
(b) Power is distributed among the legislature, executive and judiciary.
(c) Elected officials exercise supreme power in the government.
(d) Governmental power is divided between different levels of government.

Answer

(d) Governmental power is divided between different levels of government.

9. A few subjects in various Lists of the Indian Constitution are given here. Group them under the Union, State and Concurrent Lists as provided in the table below.
A. Defence
B. Police
C. Agriculture
D. Education
E. Banking
F. Forests
G. Communications
H. Trade
I. Marriages

Union List	-
State List	-
Concurrent List	-

Answer

Union List	Defence, Banking, Communications
State List	Police, Agriculture, Trade
Concurrent List	Education, Forests, Marriages

Page No: 28

10. Examine the following pairs that give the level of government in India and the powers of the government at that level to make laws on the subjects mentioned against each. Which of the following pairs is not correctly matched?

(a)	State government	State List
(b)	Central government	Union List
(c)	Central and State government	Concurrent List
(d)	Local governments	Residuary powers

Answer

(d)

Local governments

Residuary powers

11. Match List I with List II and select the correct answer using the codes given below the lists:

List I	List II
1. Union of India	A. Prime Minister
2. State	Β. Sarpanch
3. Municipal	C. Governor
4. Gram Panchayat	D. Mayor

	1	2	3	4
(a)	D	A	B	C
(b)	B	C	D	A
(c)	A	C	D	B
(d)	C	D	A	B

Answer

	1	2	3	4
(c)	A	C	D	B

12. Consider the following statements.
A. In a federation the powers of the federal and provincial governments are clearly demarcated.
B. India is a federation because the powers of the Union and State Governments are specified in the Constitution and they have exclusive jurisdiction on their respective subjects.
C. Sri Lanka is a federation because the country is divided into provinces.
D. India is no longer a federation because some powers of the states have been devolved to the local government bodies.
Which of the statements given above are correct?
(a) A, B and C
(b) A, C and D
(c) A and B only
(d) B and C only

Answer

(c) A and B only

Go Back To NCERT Solutions for Class 10 Civics

↧

NCERT Solutions for Class 10th Science: Ch 1 Chemical Reactions and Equations

February 8, 2020, 10:01 am

≫ Next: पाठ 3 लोकतंत्र और विविधता लोकतांत्रिक राजनीति के नोट्स| Class 10th

≪ Previous: NCERT Solutions for Class 10 Ch 2 Federalism Civics

NCERT Solutions for Class 10th Science: Chapter 1 Chemical Reactions and Equations

NCERT Solutions for Chapter 1 Chemical reactions and Equations is the first chapter of Class 10 Science Textbook. It covers the topic of Chemistry which covers the idea of chemicals. The topics which are covered in this chapter are Chemical equation, Balanced chemical equation, implication of a balanced chemical equation, types of chemical reactions: Combination, decomposition, displacement, double displacement, precipitation, neutralization, oxidation and reduction. We have also made NCERT Solution for Class 10 Science which includes all the textbooks solutions for textbooks. These are based on the latest pattern of CBSE. Overall, the chapter Chemical Reactions and Equations will help the students in their examination.

Study Reference for Class 10 Chapter 1 Chemical Reactions and Equations
Revision Notes for Chapter 1 Chemical Reactions and Equations Extra Questions for Chapter 1 Chemical Reactions and Equations MCQ for Chapter 1 Chemical Reactions and Equations Video for Chapter 1 Chemical Reactions and Equations

Study Reference for Class 10 Chapter 1 Chemical Reactions and Equations

In Text Questions

Page No: 6

1. Why should a magnesium ribbon be cleaned before it is burnt in air?

Answer

Magnesium is a very reactive metal. When stored, it reacts with oxygen to form a layer of magnesium oxide on its surface. This layer of magnesium oxide is quite stable and prevents further reaction of magnesium with oxygen. The magnesium ribbon is cleaned by sand paper for removing this layer so that the underlying metal can be exposed to air.

2. Write the balanced equation for the following chemical reactions.

(i) Hydrogen + Chlorine → Hydrogen chloride
(ii) Barium chloride + Aluminium sulphate → Barium sulphate + Aluminium chloride
(iii) Sodium + Water → Sodium hydroxide + Hydrogen

Answer

(i) H₂ (g) + Cl₂ (g) → 2HCl (g)

(ii) 3BaCl₂ (s) + Al₂(SO₄)₃ (s) → 3BaSO₄ (s) + 2AlCl₃ (s)

(iii) 2Na(s) + 2H₂O (l) → 2NaOH (aq) + H₂ (g)

3. Write a balanced chemical equation with state symbols for the following reactions.

(i) Solutions of barium chloride and sodium sulphate in water react to give insoluble barium sulphate and the solution of sodium chloride.
(ii) Sodium hydroxide solution (in water) reacts with hydrochloric acid solution (in water) to produce sodium chloride solution and water.

Answer

(i) BaCl₂ (aq) + Na₂SO₄ (aq) → BaSO₄ (s) + 2NaCl (aq)

(ii) NaOH (aq) + HCl (aq) → NaCL (aq) + H₂O (l)

Page No: 10

1. A solution of a substance ‘X’ is used for white washing.
(i) Name the substance ‘X’ and write its formula.
(ii) Write the reaction of the substance ‘X’ named in (i) above with water.

Answer

(i) The substance ‘X’ is calcium oxide. Its chemical formula is CaO.

(ii) Calcium oxide reacts vigorously with water to form calcium hydroxide (slaked lime).
CaO (s) + H₂O (l) → Ca(OH)₂ (aq)
Calcium Oxide (Quick Lime) + Water → Calcium Hydroxide (Slaked Lime)

2. Why is the amount of gas collected in one of the test tubes in Activity 1.7 double of the amount collected in the other? Name this gas.

Answer

Water contains two parts of hydrogen and one part oxygen. Therefore, during the electrolysis of water the amount of hydrogen gas collected in one of the test tubes is double than that of the oxygen produced and collected in the other test tube.

Page No: 13

1. Why does the colour of copper sulphate solution change when an iron nail is dipped in it?

Answer

When an iron nail dipped in the copper sulphate solution than iron displaces copper from the copper sulphate because iron is more reactive than copper. Therefore the colour of the copper sulphate solution changes.

The reaction involved here is:

Fe (s) + CuSO₄ (aq) → FeSO₄ (aq) + Cu (s)

2. Give an example of a double displacement reaction other than the one given in Activity 1.10.

Answer

2KBr (aq) + BaI₂ (aq) → 2KI (aq) + BaBr₂ (aq)

3. Identify the substances that are oxidised and the substances that are reduced in the following reactions.
(i) 4Na (s) + O₂ (g) → 2Na₂O (s)
(ii) CuO (s) + H₂ (g) → Cu (s) + H₂O (l)

Answer

(i) Sodium (Na) is oxidised as it gains oxygen and oxygen gets reduced.

(ii) Copper oxide (CuO) is reduced to copper (Cu) while hydrogen (H₂) gets oxidised to water (H₂O).

Excercise

Page No: 14

1. Which of the statements about the reaction below are incorrect?
2PbO (s) + C (s) → 2Pb (s) + CO2 (g)
(a) Lead is getting reduced.
(b) Carbon dioxide is getting oxidised.
(c) Carbon is getting oxidised.
(d) Lead oxide is getting reduced.

(i) (a) and (b)
(ii) (a) and (c)
(iii) (a), (b) and (c)
(iv) all
► (i) (a) and (b)

2. Fe₂O₃ + 2Al → Al₂O₃ + 2Fe
The above reaction is an example of a
(a) combination reaction.
(b) double displacement reaction.
(c) decomposition reaction.
(d) displacement reaction.
► (d) displacement reaction.

Page No: 15

3. What happens when dilute hydrochloric acid is added to iron filings? Tick the correct answer.
(a) Hydrogen gas and iron chloride are produced.
(b) Chlorine gas and iron hydroxide are produced.
(c) No reaction takes place.
(d) Iron salt and water are produced.

► (a) Hydrogen gas and iron chloride are produced.

4. What is a balanced chemical equation? Why should chemical equations be balanced?

Answer

A reaction which has an equal number of atoms of all the elements on both sides of the chemical equation is called a balanced chemical equation.Chemical reaction should be balanced to follow law of conservation of mass.

5. Translate the following statements into chemical equations and then balance them.

(a) Hydrogen gas combines with nitrogen to form ammonia.
(b) Hydrogen sulphide gas burns in air to give water and sulphur dioxide.
(c) Barium chloride reacts with aluminium sulphate to give aluminium chloride and a precipitate of barium sulphate.

(d) Potassium metal reacts with water to give potassium hydroxide and hydrogen gas.

Answer

(a) 3H₂ (g) + N₂ (g) → 2NH₃ (g)

(b) 2H₂S (g) + 3O₂ (g) → 2H₂O (l) + 2SO₂ (g)

(c) 3BaCl₂ (aq) + Al₂(SO₄)₃ (aq) → 2AlCl₃ (aq) + 3BaSO₄ (s)

(d) 2K (s) + 2H₂O (l) → 2KOH (aq) + H₂ (g)

6. Balance the following chemical equations.

(i) HNO₃ + Ca(OH)₂→ Ca(NO₃)₂ + H₂O
(ii) NaOH + H₂SO₄→ Na₂SO₄ + H₂O
(iii) NaCl + AgNO₃→ AgCl + NaNO₃
(iv) BaCl₂ + H₂SO₄→ BaSO₄ + HCl

Answer

(i) 2HNO₃ + Ca(OH)₂→ Ca(NO₃)₂ + 2H₂O
(ii) 2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O
(iii) NaCl + AgNO₃ → AgCl + NaNO₃
(iv) BaCl₂ + H₂SO₄ → BaSO₄ + 2HCl

7. Write the balanced chemical equations for the following reactions.

(a) Calcium hydroxide + Carbon dioxide → Calcium carbonate + Water
(b) Zinc + Silver nitrate → Zinc nitrate + Silver
(c) Aluminium + Copper chloride → Aluminium chloride + Copper
(d) Barium chloride + Potassium sulphate → Barium sulphate + Potassium chloride

Answer

(a) Ca(OH)₂ + CO₂→ CaCO₃ + H₂O

(b) Zn + 2AgNO₃→ Zn(NO₃)₂ + 2Ag

(c) 2Al + 3CuCl₂→ 2AlCl₃ + 3Cu

(d) BaCl2 + K₂SO₄→ BaSO₄ + 2KCl

8. Write the balanced chemical equation for the following and identify the type of reaction in each case.

(a)Potassium bromide (aq) + Barium iodide (aq) → Potassium iodide (aq) + Barium bromide(s)
(b) Zinc carbonate (s) → Zinc oxide (s) + Carbon dioxide (g)
(c) Hydrogen (g) + Chlorine (g) → Hydrogen chloride (g)
(d) Magnesium (s) + Hydrochloric acid (aq) → Magnesium chloride (aq) + Hydrogen (g)

Answer

(a) 2KBr (aq) + BaI₂ (aq) → 2KI (aq) + BaBr₂ (s): Double displacement reaction

(b) ZnCO₃ (s) → ZnO (s) + CO₂ (g): Decomposition reaction

(c) H₂ (g) + Cl₂ (g) → 2HCl (g): Combination reaction

(d) Mg (s) + 2HCl (aq) → MgCl₂ (aq) + H₂ (g) : Displacement Reaction

9. What does one mean by exothermic and endothermic reactions? Give examples.

Answer

Chemical reactions that release energy in the form of heat, light, or sound are called exothermic reactions.

Example: C (g) + O₂ (g) → CO₂ + Heat Energy

Reactions that absorb energy or require energy in order to proceed are called endothermic reactions.

Example:

10. Why is respiration considered an exothermic reaction? Explain.

Answer

Respiration is considered as an exothermic reaction because in respiration oxidation of glucose takes place which produces large amount of heat energy.
C₆H₁₂O₆ (aq) + 6O₂ (g) → 6CO₂ (g) + 6H₂O (l) + Energy

11. Why are decomposition reactions called the opposite of combination reactions? Write equations for these reactions.

Answer

Decomposition reactions are those in which a compound breaks down to form two or more substances. These reactions require a source of energy to proceed. Thus, they are the exact opposite of combination reactions in which two or more substances combine to give a new substance with the release of energy.For Example:
Decomposition Reaction:

Combination Reaction:
CaO (s) + H₂O (l) → Ca(OH)₂ (aq)

Page No: 16

12. Write one equation each for decomposition reactions where energy is supplied in the form of heat, light or electricity.

Answer

13. What is the difference between displacement and double displacement reactions? Write equations for these reactions.

Answer

In a displacement reaction, a more reactive element replaces a less reactive element from a compound.
For Example: CuSo₄ (aq) + Zn (s) → ZnSO₄ (aq) + Cu (s)
In a double displacement reaction, two atoms or a group of atoms switch places to form new compounds.

For Example: Na₂SO₄ (aq) + BaCl₂ (aq) → BaSO₄ (s) + 2NaCl (aq)

14. In the refining of silver, the recovery of silver from silver nitrate solution involved displacement by copper metal. Write down the reaction involved.

Answer

2AgNO₃ (aq) + Cu (s) → Cu(NO₃)₂ (aq) + 2Ag (s)
Silver Nitrate + Copper → Copper Nitrate + Silver

15. What do you mean by a precipitation reaction? Explain by giving examples.

Answer

A reaction in which an insoluble solid (called precipitate) is formed is called a precipitation reaction.For Example:
Na₂CO₃ (aq) + CaCl₂ (aq) → CaCO₃ (s) + 2NaCl (aq)
Sodium Carbonate + Calcium Chloride → Calcium Carbonate + Sodium Chloride
In this reaction, calcium carbonate is obtained as a precipitate. Hence, it is a precipitation reaction.

16. Explain the following in terms of gain or loss of oxygen with two examples each.
(a) Oxidation
(b) Reduction

Answer

Oxidation Reaction: It is a chemical reaction in which gain of oxygen or loss of hydrogen takes place.

Reduction Reaction: It is a chemical reaction in which loss of oxygen or gain of hydrogen takes place.

17. A shiny brown-coloured element ‘X’ on heating in air becomes black in colour. Name the element ‘X’ and the black coloured compound formed.

Answer

‘X’ is copper (Cu) and the black-coloured compound formed is copper oxide (CuO). The equation of the reaction involved on heating copper is given below.

18. Why do we apply paint on iron articles?

Answer

Iron articles are painted because it prevents them from rusting. When painted, the contact of iron articles from moisture and air is cut off. Hence, rusting is prevented.

19. Oil and fat containing food items are flushed with nitrogen. Why?

Answer

Oil and fat containing food items flushed with nitrogen because nitrogen acts as an antioxidant and it prevents them from being oxidised.

20. Explain the following terms with one example each.
(a) Corrosion
(b) Rancidity

Answer

Corrosion is defined as a process where materials, usually metals, deteriorate as a result of a chemical reaction with air, moisture, chemicals, etc.
For example, iron, in the presence of moisture, reacts with oxygen to form hydrated iron oxide.
4Fe + 3O₂ + nH₂O → 2Fe₂O₃.nH₂O

Rancidity is the process of oxidation of fats and oils that can be easily noticed by the change in taste and smell is known as rancidity.
For example, the taste and smell of butter changes when kept for long.

State the law which is kept in mind while we balance a chemical equation.

Law of conservation of mass. Mass can neither be created nor be destroyed during a chemical reaction.

What is basic difference between a physical change and a chemical change?

In a physical change, no new substance is formed. In a chemical change, new substance is formed.

What is meant by a chemical reaction?

A process in which two or more substances react to form some other new substances with new set of properties is called a chemical reaction.

Is burning of a candle, a physical change or a chemical change?

Burning of candle is both chemical change and physical change.

Why are decomposing reactions called the opposite of combination reactions?

In combination reactions, two substances combine to form one compound and in decomposition reactions, a compound breaks down into two or more substances, so they are opposite to each other.

Go Back To NCERT Solutions for Class 10th Science

↧

पाठ 3 लोकतंत्र और विविधता लोकतांत्रिक राजनीति के नोट्स| Class 10th

February 8, 2020, 10:24 am

≫ Next: NCERT Solutions for Class 10th Science: Ch 2 Acids, Bases and Salts

≪ Previous: NCERT Solutions for Class 10th Science: Ch 1 Chemical Reactions and Equations

NCERT Solutions for Class 10th: पाठ 3 - लोकतंत्र और विविधता (Loktantr aur Vividhta) Loktantrik Rajniti

अमरीका में नागरिक अधिकार आंदोलन

• घटनाओं और सुधार आंदोलनों का एक सिलसिला जिसका उद्देश्य एफ्रो-अमरीकी लोगों के विरुद्ध होने वाले नस्ल आधारित भेदभाव को मिटाना था।

• मार्टिन लूथर किंग जूनियर की अगुवाई में लड़े गए इस आंदोलन (1954-1968) का स्वरूप पूरी तरह अहिंसक था।

समानताएँ, असमानताएँ और विभाजन

सामाजिक विभिन्नताएँ क्या हैं?

• सामाजिक विभिन्नताएँ जन्म पर आधारित या व्यक्तिगत पसंद या चुनाव के आधार पर सामाजिक पहचान है।

सामाजिक भेदभाव की उत्पत्ति

• अधिकांश सामाजिक भेदभाव जन्म पर आधारित हैं।

• कुछ व्यक्तिगत पसंद या चुनाव पर आधारित हैं।

सामाजिक विभाजन

• यह सामाजिक विषमताओं जैसे धर्म, जाति आदि पर आधारित संघर्ष की स्थिति है।

• हर सामाजिक विभिन्नता सामाजिक विभाजन का रूप नहीं लेती। सामाजिक विभिन्नताएँ लोगों के बीच बँटवारे का एक बड़ा कारण होती ज़रूर हैं लेकिन यही विभिन्नताएँ कई बार अलग-अलग तरह के लोगों के बीच पुल का काम भी करती हैं।

विभिन्नताओं में सामंजस्य

• सामाजिक विभाजन तब होता है जब कुछ सामाजिक अंतर दूसरी अनेक विभिन्नताओं से ऊपर और बड़े हो जाते हैं।

विभिन्नताओं में टकराव

• अगर एक-सी सामाजिक असमानताएँ कई समूहों में मौजूद हों तो फिर एक समूह के लोगों के लिए दूसरे समूहों से अलग पहचान बनाना मुश्किल हो जाता है।

सामाजिक विभाजनों की राजनीति

• लोकतंत्र में विभिन्न राजनीतिक पार्टियों के बीच प्रतिद्वंद्विता का माहौल होता है।

• प्रतिद्वंद्विता समाज को विभाजित करती है और उन्हें राजनीतिक विभाजनों में बदल देती है जो अंततः संघर्ष, हिंसा या किसी देश के विघटन की ओर ले जाती है।

सामाजिक विभाजनों की राजनीति का परिणाम तीन चीज़ों पर निर्धारित करता है-

• पहली चीज है लोगों में अपनी पहचान के प्रति आग्रह की भावना।
→ अगर लोग खुद को सबसे विशिष्ट और अलग मानने लगते हैं तो उनके लिए दूसरों के साथ तालमेल बैठाना बहुत मुश्किल हो जाता है।

• दूसरी महत्वपूर्ण चीज़ है कि किसी समुदाय की माँगों को राजनीतिक दल कैसे उठा रहे हैं।
→ संविधान के दायरे में आने वाली और दूसरे समुदाय को नुकसान न पहुँचाने वाली माँगों को मान लेना आसान है।

• तीसरी चीज़ है सरकार का रुख।
→ अगर शासन सत्ता में साझेदारी करने को तैयार हो और अल्पसंख्यक समुदाय की उचित माँगों को पूरा करने का प्रयास ईमानदारी से किया जाए तो सामाजिक विभाजन मुल्क के लिए खतरा नहीं बनते।

↧

NCERT Solutions for Class 10th Science: Ch 2 Acids, Bases and Salts

February 8, 2020, 10:26 am

≫ Next: NCERT Solutions for Class 10th: Ch 3 Metals and Non-metals Science

≪ Previous: पाठ 3 लोकतंत्र और विविधता लोकतांत्रिक राजनीति के नोट्स| Class 10th

NCERT Solutions for Class 10th Science: Chapter 2 Acids, Bases and Salts

The definitions of Acids and Bases in terms of furnishing of H⁺ and OH^- ions, General properties, examples and uses, concept of pH scale (Definition relating to logarithm not required), importance of pH in everyday life; preparation and uses of Sodium Hydroxide, Bleaching powder, Baking soda, Washing soda and Plaster of Paris are the topics which will be studied in Class 10 Chapter 2 Acids, Bases and Salts. These topics are very important for examination. NCERT Solutions for Chapter 2 Acids, Bases and Salts is helpful in last minute question and Answers which has been provided here. This is based according to the latest pattern released by CBSE.

Study Reference for Class 10 Chapter 2 Acids, Bases and Salts
Revision Notes for Chapter 2 Acids, Bases and Salts Extra Questions for Chapter 2 Acids, Bases and Salts MCQ Test for Chapter 2 Acids, Bases and Salts Video for Chapter 2 Acids, Bases and Salts

Study Reference for Class 10 Chapter 2 Acids, Bases and Salts

In Text Questions

Page No: 18

1. You have been provided with three test tubes. One of them contains distilled water and the other two contain an acidic solution and a basic solution, respectively. If you are given only red litmus paper, how will you identify the contents of each test tube?

Answer

If the colour of red litmus does not change then it is acid. If the colour of red litmus changes to blue then it is base. If there is slight change in the colour of red litmus (such as purple) then it is distilled water.

Page No: 22

1. Why should curd and sour substances not be kept in brass and copper vessels?

Answer

Curd and other sour substances contain acids. Therefore, when they are kept in brass and copper vessels, the metal reacts with the acid to liberate hydrogen gas and harmful products, thereby spoiling the food.

2. Which gas is usually liberated when an acid reacts with a metal? Illustrate with an example. How will you test for the presence of this gas?

Answer

Hydrogen gas is usually liberated when an acid reacts with metal.

Take few pieces of zinc granules and add 5 ml of dilute H2SO4. Shake it and pass the gas produced into a soap solution. The bubbles of the soap solution are formed. These soap bubbles contain hydrogen gas.
H₂SO₄ + Zn → ZnSO₄ + H₂↑
We can test the evolved hydrogen gas by its burning with a pop sound when a candle is brought near the soap bubbles.

3. Metal compound A reacts with dilute hydrochloric acid to produce effervescence. The gas evolved extinguishes a burning candle. Write a balanced chemical equation for the reaction if one of the compounds formed is calcium chloride.

Answer

CaCO₃ (s) + 2HCl (aq) → CaCl₂ (aq) + CO₂ (g) + H₂O (l)
Calcium Carbonate + Hydrochloric acid → Calcium Chloride + Carbon dioxide + Water

Page No: 25

1. Why do HCl, HNO₃, etc., show acidic characters in aqueous solutions while solutions of compounds like alcohol and glucose do not show acidic character?

Answer

When HCl or HNO₃ are mixed with water then they dissolve in water to form H⁺ or H₃O⁺ ions which shows their acidic character. For example just see the following reactions

HCl (aq) → H⁺ + Cl^-

H⁺ + H₂O → H₃O⁺

When alcohols and glucose are mixed with water then they do not dissolve to form ions. Hence they do not show acidic character.

2. Why does an aqueous solution of an acid conduct electricity?

Answer

The presence of hydrogen (H⁺) or hydronium (H₃O⁺) ions in the aqueous solution of an acid are responsible for conducting electricity.

3. Why does dry HCl gas not change the colour of the dry litmus paper?

Answer

Dry HCl gas not change the colour of the dry litmus paper because it has no Hydrogen ions (H⁺) in it.

4. While diluting an acid, why is it recommended that the acid should be added to water and not water to the acid?

Answer

Since the process of dissolving an acid in water is exothermic, it is always recommended that acid should be added to water. If it is done the other way, then it is possible that because of the large amount of heat generated, the mixture splashes out and causes burns.

5. How is the concentration of hydronium ions (H₃O⁺) affected when a solution of an acid is diluted?

Answer

When an acid is diluted, the concentration of hydronium ions (H₃O⁺) per unit volume decreases. This means that the strength of the acid decreases.

6. How is the concentration of hydroxide ions (OH⁻) affected when excess base is dissolved in a solution of sodium hydroxide?

Answer

The concentration of hydroxide ions (OH⁻) would increase when excess base is dissolved in a solution of sodium hydroxide.

Page No: 28

1. You have two solutions, A and B. The pH of solution A is 6 and pH of solution B is 8. Which solution has more hydrogen ion concentration? Which of this is acidic and which one is basic?

Answer

A pH value of less than 7 indicates an acidic solution, while greater than 7 indicates a basic solution. Therefore, the solution with pH = 6 is acidic and has more hydrogen ion concentration than the solution of pH = 8 which is basic.

2. What effect does the concentration of H⁺ (aq) ions have on the nature of the solution?

Answer

If the concentration of H⁺ (aq) ions is increased (>10-7) then the solution become acidic and if the concentration of H⁺ (aq) ions is decreased (<10-7) then the solution become basic in nature.

3. Do basic solutions also have H⁺ (aq) ions? If yes, then why are these basic?

Answer

Yes, basic solution also has H⁺ ions. However, their concentration is less as compared to the concentration of OH^- ions that makes the solution basic.

4. Under what soil condition do you think a farmer would treat the soil of his fields with quick lime (calcium oxide) or slaked lime (calcium hydroxide) or chalk (calcium carbonate)?

Answer

If the soil is acidic and improper for cultivation, then to increase the basicity of soil, the farmer would treat the soil with quick lime or slaked lime or chalk.

Page No: 33

1. What is the common name of the compound CaOCl₂?
► Bleaching Powder.

2. Name the substance which on treatment with chlorine yields bleaching powder?
► Calcium hydroxide [Ca(OH)₂]

3. Name the sodium compound which is used for softening hard water.
► Washing soda (Na₂CO₃.10H₂O)

4. What will happen if a solution of sodium hydrocarbonate is heated? Give the equation of the reaction involved.

Answer

When sodium hydrogen carbonate is heated then sodium carbonate and water is formed along with the evolution of carbon dioxide gas.

5. Write an equation to show the reaction between Plaster of Paris and water.

Answer

Page No: 34

Exercise

1. A solution turns red litmus blue, its pH is likely to be
(a) 1
(b) 4
(c) 5
(d) 10
► (d) 10

2. A solution reacts with crushed egg-shells to give a gas that turns lime-water milky. The solution contains
(a) NaCl

(b) HCl

(d) KCl

► (b) HCl

3. 10 mL of a solution of NaOH is found to be completely neutralised by 8 mL of a given solution of HCl. If we take 20 mL of the same solution of NaOH, the amount of HCl solution (the same solution as before) required to neutralise it will be
(a) 4 mL

(b) 8mL

(d) 16 mL

► (d) 16 mL

4. Which one of the following types of medicines is used for treating indigestion?
(a) Antibiotic
(b) Analgesic
(c) Antacid
(d) Antiseptic
► (c) Antacid

5, Write word equations and then balanced equations for the reaction taking place when −
(a) dilute sulphuric acid reacts with zinc granules.
(b) dilute hydrochloric acid reacts with magnesium ribbon.
(c) dilute sulphuric acid reacts with aluminium powder.
(d) dilute hydrochloric acid reacts with iron filings.

Answer

(a) H₂SO₄ (aq) + Zn (s) → ZnSO₄ (aq) + H₂ (g)

(b) 2HCl (aq) + Mg (s) → MgCl₂ (aq) + H₂ (g)

(c) 3H₂SO₄ (aq) + 2Al (s) → Al₂(SO₄)₃ (aq) + 3H₂ (g)

(d) 6HCl (aq) + 2Fe (s) → 2FeCl₃ (aq) + 3H₂ (g)

6. Compounds such as alcohols and glucose also contain hydrogen but are not categorized as acids. Describe an activity to prove it.

Answer

Two nails are fitted on a cork and are kept it in a 100 mL beaker. The nails are then connected to the two terminals of a 6-volt battery through a bulb and a switch. Some dilute HCl is poured in the beaker and the current is switched on. The same experiment is then performed with glucose solution and alcohol solution.

Observations:
It will be observed that the bulb glows in the HCl solution and does not glow in the glucose solution.

Result:
HCl dissociates into H⁺and Cl⁻ions. These ions conduct electricity in the solution resulting in the glowing of the bulb. On the other hand, the glucose solution does not dissociate into ions. Therefore, it does not conduct electricity.

Conclusion:
From this activity, it can be concluded that all acids contain hydrogen but not all compounds containing hydrogen are acids.
That is why, though alcohols and glucose contain hydrogen, they are not categorised as acids.

7. Why does distilled water not conduct electricity, whereas rain water does?

Answer

Distilled water cannot conduct electricity because it does not contain ions while rain water conducts electricity as it contains ions due presence of dissolved salts in it.

8. Why do acids not show acidic behaviour in the absence of water?

Answer

Acids do not show acidic behaviour in the absence of water because the dissociation of hydrogen ions from an acid occurs in the presence of water only.

9. Five solutions A, B, C, D and E when tested with universal indicator showed pH as 4, 1, 11, 7 and 9, respectively. Which solution is
(a) neutral?
(b) strongly alkaline?
(c) strongly acidic?
(d) weakly acidic?
(e) weakly alkaline?
Arrange the pH in increasing order of hydrogen-ion concentration.

Answer

(a) Neutral →Solution D with pH 7
(b) Strongly alkaline →Solution C with pH 11
(c) Strongly acidic →Solution B with pH 1
(d) Weakly acidic →Solution A with pH 4
(e) Weakly alkaline →Solution E with pH 9
The pH can be arranged in the increasing order of the concentration of hydrogen ions as: 11 < 9 < 7 < 4 < 1.

10. Equal lengths of magnesium ribbons are taken in test tubes A and B. Hydrochloric acid (HCl) is added to test tube A, while acetic acid (CH₃COOH) is added to test tube B. In which test tube will the fizzing occur more vigorously and why?

Answer

The fizzing will occur strongly in test tube A, in which hydrochloric acid (HCl) is added. This is because HCl is a stronger acid than CH₃COOH and therefore produces hydrogen gas at a faster speed due to which fizzing occurs.

11. Fresh milk has a pH of 6. How do you think the pH will change as it turns into curd? Explain your answer.

Answer

The pH of milk is 6. As it changes to curd, the pH will reduce because curd is acidic in nature. The acids present in it decrease the pH.

12.A milkman adds a very small amount of baking soda to fresh milk.
(a) Why does he shift the pH of the fresh milk from 6 to slightly alkaline?
(b) Why does this milk take a long time to set as curd?

Answer

(a) The milkman shifts the pH of the fresh milk from 6 to slightly alkaline because in alkaline condition, milk does not set as curd easily.

(b) Since this milk is slightly basic than usual milk, acids produced to set the curd are neutralized by the base. Therefore, it takes a longer time for the curd to set.

13. Plaster of Paris should be stored in a moisture-proof container. Explain why?

Answer

The Plaster of Paris should be stored in a moisture-proof container as it absorbs water from moisture and turn into hard substance (Gypsum) as shown in following chemical equation.

14. What is a neutralization reaction? Give two examples.

Answer

A reaction in which an acid and base react with each other to give a salt and water is termed as neutralization reaction.For Example:
(i) NaOH + HCl → NaCl + H₂O
(ii) HNO₃ + KOH → KNO₃ + H₂O

15. Give two important uses of washing soda and baking soda.

Answer

Two important uses of washing soda are:
→ It is used in glass, soap, and paper industries.
→ It is used to remove permanent hardness of water.

Two important uses of baking soda are:
→ It is used as baking powder. Baking powder is a mixture of baking soda and a mild acid known as tartaric acid. When it is heated or mixed in water, it releases CO2 that makes bread or cake fluffy.
→ It is used in soda-acid fire extinguishers.

Why does tooth decay start when the pH of mouth is lower than 5.5?

At lower pH below 5.5, the calcium phosphate of enamel of tooth is corroded.

What would be the colour of litmus in a solution of sodium carbonate?

The colour of litmus in a solution of sodium carbonate is blue.

What is the common name of the compound CaOCl₂?

Bleaching powder.

What is bleaching powder ? How is it prepared ?

Bleaching Powder is Calcium Oxychloride. It is prepared by the action of chlorine on dry slaked lime.

Go Back To NCERT Solutions for Class 10th Science

↧

OJEE 2020 Application process begins at ojee.nic.in, Exam To Be Held In first week of May

OJEE Eligibility Criteria

Use CBSE Exam Locator App to find your exam center

Steps to use CBSE Exam Locator App

NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Exercise 13.2

NCERT Solutions for Chapter 14 Factorisation Class 8 Mathematics

NCERT Solutions for Chapter 16 Playing with Numbers Class 8 Mathematics

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.1

NCERT Solutions for Chapter 1 Integers Class 7 Mathematics

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.2

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.3

NCERT Solutions for Chapter 2 Fractions and Decimals Class 7 Mathematics

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.4

NCERT Solutions for Chapter 3 Data Handling Class 7 Mathematics

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Exercise 14.5

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.1

NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Exercise 3.2

NCERT Solutions for Class 10 Ch 1 Power Sharing Civics Social Studies (S.St)

NCERT Solutions for Class 10 Ch 2 Federalism Civics Social Studies (S.St)

NCERT Solutions for Class 10th Science: Chapter 1 Chemical Reactions and Equations

State the law which is kept in mind while we balance a chemical equation.

What is basic difference between a physical change and a chemical change?

What is meant by a chemical reaction?

Is burning of a candle, a physical change or a chemical change?

Why are decomposing reactions called the opposite of combination reactions?

NCERT Solutions for Class 10th: पाठ 3 - लोकतंत्र और विविधता (Loktantr aur Vividhta) Loktantrik Rajniti

NCERT Solutions for Class 10th Science: Chapter 2 Acids, Bases and Salts

Why does tooth decay start when the pH of mouth is lower than 5.5?

What would be the colour of litmus in a solution of sodium carbonate?

What is the common name of the compound CaOCl2?

What is bleaching powder ? How is it prepared ?

What is the common name of the compound CaOCl₂?