NCERT Solutions for Class 7 Maths Ch 12 Algebraic Expressions
In this page, we have provided Chapter 12 Algebraic Expressions NCERT Solutions for Class 7 Maths through which you can high marks in the exams and learn efficiently. These NCERT Solutions for Class 7 are accurate and detailed through which you can clear your doubts.
Exercise 12.1
1. Get the algebraic expressions in the following cases using variables, constants, and arithmetic operations:
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of m and n.
(vii) A product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Answer
(i) y - z
(ii) (x + y)/2
(iii) z2
(iv) pq/4
(v) x2 + y2
(vi) 3mn + 5
(vii) 10 - yz
(viii) ab - (a + b)
2. (i) Identify the terms and their factors in the following expressions, show the terms and factors by tree diagram:
(a) x – 3
(b) 1 + x + x2
(c) y – y3
(d) 5xy2 + 7x2y
(e) -ab + 2b2– 3a2
Answer
(ii) Identify the terms and factors in the expressions given below:
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y2
(d) xy + 2x2y2
(e) pq + q
(f) 1.2ab - 2.4b + 3.6a
(h) 0.1 p2 + 0.2q2
Answer
(a) -4x+ 5
Terms: -4x,5
Factors: -4,x ; 5
(b) -4x + 5y
Terms: -4x, 5y
Factors: -4,x ; 5,y
(c) 5y + 3y2
Terms: 5y,3y2
Factors: 5, y ; 3,y,y
(d) xy+2x2y2
Terms: xy,2x2y2
Factors: x,y ; 2x,x,y,y
(e) pq+q
Terms: pq,q
Factors: p,q ; q
(f) 1.2ab-2.4b+3.6a
Terms: 1,2ab.-2.4b,3 6a
Factors: 1.2.a.b ; -2.4,6 ; 3.6,a
(h) 0.1p2+0.2q2
Terms: 0.1 p2,0.2q2
Factors: 0. 1,p,p, ; 0.2, q,q
3. Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 - 3t2
(ii) 1 + t + t2 + t2
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p2q2 + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r2
(viii) 2(l+b)
(ix) 0.1y + 0.01y2
Answer
| S.No. | Expression | Terms | Numerical Coefficient |
| (i) | 5-3t2 | -3t1 | -3 |
| (ii) | 1+t+t2+t3 | t | 1 |
| t2 | 1 | ||
| t3 | 1 | ||
| (iii) | x + 2xy + 3y | x | 1 |
| 2xy | 2 | ||
| 3y | 3 | ||
| (iv) | 100m+1000n | 100 m | 100 |
| 1000 n | 1000 | ||
| (v) | -p2q2+7 pq | -p2q2 | -1 |
| 7 pq | 7 | ||
| (vi) | 1.2a+0.8b | 1.2 a | 1.2 |
| 0.8b | 0.8 | ||
| (vii) | 3.14 r2 | 3.14 r2 | 3.14 |
| (viii) | 2 (l + b) = 2l+ 2b | 2l | 2 |
| 2b | 2 | ||
| (ix) | 0.1y + 0.01y2 | 0.1y | 0.1 |
| 0.01y2 | 0.01 |
4. (a) Identify terms which contain x and give the coefficient of x.
(i) y2x + y
(ii) 13y2 - 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy2 + x25
(vii) 7x + xy2
(b) Identify terms which contain y2 and give the coefficient of y2.
(i) 8 - xy2
(ii) 5y2 + 7x
(iii) 2x2y - 15xy2 + 7y2
Answer
| S.No. | Expression | Term with factor x | Coefficient of x |
| (i) | y2x + y | y2 x | y |
| (ii) | 13y2 -8yx | -8 yx | -8 y |
| (iii) | x + y + 2 | x | 1 |
| (iv) | 5 + z + zx | zx | z |
| (v) | 1 + x + xy | x | 1 |
| xy | 1 | ||
| (vi) | 12xy2 +25 | 12 xy2 | 12y2 |
| (vii) | 7x+xy2 | xy2 | y2 |
| 7x | 7 |
| S. No. | Expression | Term containing y2 | Coefficient of y2 |
| (i) | 8-xy2 | -xy2 | -x |
| (ii) | 5y+7x | 5y2 | 5 |
| (iii) | 2x2y-15xy2 + 7y2 | -15xy2 | -15x |
| 7y2 | 7 |
5. Classify into monomials, binomials and trinomials:
(i) 4y - 7x
(ii) y2
(iii) x + y - xy
(iv) 100
(v) ab - a - b
(vi) 5 - 3t
(vii) 4p2q - 4pq2
(viii) 7mn
(ix) z2 - 3z + 8
(x) a2 + b2
(xi) z2 + z
(xii) 1 + x + x2
Answer
| S.No. | Expression | Type of Polynomial |
| (i) | 4y-7z | Binomial |
| (ii) | y2 | Monomial |
| (iii) | x+y-xy | Trinomial |
| (iv) | 100 | Monomial |
| (v) | ab-a-b | Trinomial |
| (vi) | 5-3t | Binomial |
| (vii) | 4p2q-4pq2 | Binomial |
| (viii) | 7mn | Monomial |
| (ix) | z2-3z + 8 | Trinomial |
| (x) | a2 + b2 | Binomial |
| (xi) | z2 +z | Binomial |
| (xii) | 1 + x + x2 | Trinomial |
6. State whether a given pair of terms is of like or unlike terms:
(i) 1,100
(ii) ![]()
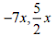
(iii) -29x, -29y
(iv) 14xy, 42 yx
(v) 4m2p, 4mp2
(vi) 12xz, 12x2 z2
Answer
| S.No. | Pair of terms | Like / Unlike terms |
| (i) | 1, 100 | Like terms |
| (ii) | 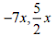| Like terms |
| (iii) | -29x,-29y | Unlike terms |
| (iv) | 14xy,42yx | Like terms |
| (v) | 4m2p,4mp2 | Unlike terms |
| (vi) | 12xz,12x2z2 | Unlike terms |
7. Identify like terms in the following:
(a) -xy2, -4yx2, 8x2, 2xy2, 7y, -11x2 - 100x, - 11yx, 20x2y, -6x2, y, 2xy, 3x
Answer
(i) -xy2,2 xy2
(ii) -4yx2 , 20x2y
(iii) 8x2,-11x2,-6x2
(iv) 7y, y
(v) -100x, 3x
(vi) -11yx, 2xy
(b) 10pq, 7p, 8q, -p2q2, -7qp, -100q, -23, 12q2p2, -5p2, 41,2405 p, 78qp, 13p2q, qp2, 701p2
Answer
(i) 10 pq - 7 pq,78 pq
(ii) 7p, 2405 p
(iii) 8q,- 100q
(iv) -p2q2, 12p2q2
(v) -12,41
(vi) -5p2,701p2
(vii) 13 p2q,qp2
Exercise 12.2
1. Simplify combining like terms:
(i) 21b – 32 + 7b – 20b
Answer
When term have the same algebraic factors, they are like terms.
Then,
= (21b + 7b – 20b) – 32
= b (21 + 7 – 20) – 32
= b (28 - 20) – 32
= b (8) - 32
= 8b - 32
(ii) – z2 + 13z2– 5z + 7z3 – 15z
Answer
When term have the same algebraic factors, they are like terms.
Then,
= 7z3 + (-z2 + 13z2) + (-5z – 15z)
= 7z3 + z2 (-1 + 13) + z (-5 - 15)
= 7z3 + z2 (12) + z (-20) + 7z3
= 7z3 + 12z2– 20z + 7z3
(iii) p – (p – q) – q – (q – p)
Answer
When term have the same algebraic factors, they are like terms.
Then,
= p – p + q – q – q + p
= p – q
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
Answer
When term have the same algebraic factors, they are like terms.
Then,
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
= a (1 – 1- 1) + b (-2 + 1 + 1) + ab (-1 -1 + 3)
= a (1 - 2) + b (-2 + 2) + ab (-2 + 3)
= a (1) + b (0) + ab (1)
= a + ab
(v) 5x2y – 5x2 + 3yx2– 3y2 + x2– y2 + 8xy2– 3y2
Answer
When term have the same algebraic factors, they are like terms.
Then,
= 5x2y + 3yx2– 5x2 + x2– 3y2– y2– 3y2
= x2y (5 + 3) + x2 (- 5 + 1) + y2 (-3 – 1 -3) + 8xy2
= x2y (8) + x2 (-4) + y2 (-7) + 8xy2
= 8x2y - 4x2– 7y2 + 8xy2
(vi) (3y2 + 5y – 4) – (8y – y2– 4)
Answer
When term have the same algebraic factors, they are like terms.
Then,
= 3y2 + 5y – 4 – 8y + y2 + 4
= 3y2 + y2 + 5y – 8y – 4 + 4
= y2 (3 + 1) + y (5 - 8) + (-4 + 4)
= y2 (4) + y (-3) + (0)
= 4y2– 3y.
2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 3mn + (-5mn) + 8mn + (- 4mn)
= 3mn – 5mn + 8mn – 4mn
= mn (3 – 5 + 8 - 4)
= mn (11 - 9)
= mn (2)
= 2mn
(ii) t – 8tz, 3tz – z, z – t
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= t – 8tz + (3tz - z) + (z - t)
= t – 8tz + 3tz – z + z - t
= t – t – 8tz + 3tz – z + z
= t (1 - 1) + tz (- 8 + 3) + z (-1 + 1)
= t (0) + tz (- 5) + z (0)
= - 5tz
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= - 7mn + 5 + 12mn + 2 + (9mn - 8) + (- 2mn - 3)
= - 7mn + 5 + 12mn + 2 + 9mn – 8 - 2mn - 3
= - 7mn + 12mn + 9mn – 2mn + 5 + 2 – 8 – 3
= mn (-7 + 12 + 9 - 2) + (5 + 2 – 8 - 3)
= mn (- 9 + 21) + (7 - 11)
= mn (12) – 4
= 12mn - 4
(iv) a + b – 3, b – a + 3, a – b + 3
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= a + b – 3 + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= a – a + a + b + b – b – 3 + 3 + 3
= a (1 – 1 + 1) + b (1 + 1 - 1) + (-3 + 3 + 3)
= a (2 -1) + b (2 -1) + (-3 + 6)
= a (1) + b (1) + (3)
= a + b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 14x + 10y – 12xy – 13 + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= 14x – 7x + 10y– 10y – 12xy + 8xy + 4xy – 13 + 18
= x (14 - 7) + y (10 - 10) + xy(-12 + 8 + 4) + (-13 + 18)
= x (7) + y (0) + xy(0) + (5)
= 7x + 5
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 5m – 7n + (3n – 4m + 2) + (2m – 3mn - 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5
= m (5 - 4 + 2) + n (-7 + 3) – 3mn + (2 - 5)
= m (3) + n (-4) – 3mn + (-3)
= 3m – 4n – 3mn - 3
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 4x2y + (-3xy2) + (-5xy2) + 5x2y
= 4x2y + 5x2y – 3xy2– 5xy2
= x2y (4 + 5) + xy2 (-3 - 5)
= x2y (9) + xy2 (- 8)
= 9x2y – 8xy2
(viii) 3p2q2– 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 3p2q2– 4pq + 5 + (- 10p2q2) + 15 + 9pq + 7p2q2
= 3p2q2– 10p2q2 + 7p2q2– 4pq + 9pq + 5 + 15
= p2q2 (3 -10 + 7) + pq (-4 + 9) + (5 + 15)
= p2q2 (0) + pq (5) + 20
= 5pq + 20
(ix) ab – 4a, 4b – ab, 4a – 4b
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= ab – 4a + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= ab (1 -1) + a (4 - 4) + b (4 - 4)
= ab (0) + a (0) + b (0)
= 0
(x) x2– y2– 1, y2– 1 – x2, 1 – x2– y2
Answer
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= x2– y2– 1 + (y2– 1 – x2) + (1 – x2– y2)
= x2– y2– 1 + y2– 1 – x2 + 1 – x2– y2
= x2– x2– x2– y2 + y2– y2– 1 – 1 + 1
= x2 (1 – 1- 1) + y2 (-1 + 1 - 1) + (-1 -1 + 1)
= x2 (1 - 2) + y2 (-2 +1) + (-2 + 1)
= x2 (-1) + y2 (-1) + (-1)
= -x2– y2 -1
3. Subtract:
(i) -5y2 from y2
Answer
y2 - (-5y2) = y2 + 5y2 = 6y2
(ii) 6xy from -12xy
Answer
-12xy -(6xy) = -12xy - 6xy = -18xy
(iii) (a - b) from (a + b)
Answer
(a + b)-(a -b) = a + b -a + b
= a - a + b + b = 2b
(iv) a (b - 5) from b (5 - a)
Answer
= b (5 - a)-a (b -5)
= 5b - ab - ab + 5a
= 5b - 2ab+5a
= 5a + 5b -2ab
(v) -m2 + 5mn from 4m2 - 3mn + 8
Answer
= 4m2 - 3mn + 8 - (- m2 + 5mn)
= 4m2 - 3mn + 8 + m2 - 5mn
= 4m2 + m2 - 3mn - 5mn + 8
= 5m2 - 8mn + 8
(vi) -x2 +10x - 5 from 5x-10
Answer
= 5x – 10 – (-x2 + 10x - 5)
= 5x – 10 + x2– 10x + 5
= x2 + 5x – 10x – 10 + 5
= x2– 5x - 5
(vii) 5a2 - 7ab + 5b2 from 3ab - 2a2 - 2b2
Answer
= 3ab – 2a2– 2b2– (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2
= 3ab + 7ab – 2a2– 5a2– 2b2– 5b2
= 10ab – 7a2– 7b2
(viii) 4pq - 5q2 - 3p2 from 5p2 + 3q2 - pq
Answer
= 5p2 + 3q2– pq – (4pq – 5q2– 3p2)
= 5p2 + 3q2– pq – 4pq + 5q2 + 3p2
= 5p2 + 3p2 + 3q2 + 5q2– pq – 4pq
= 8p2 + 8q2– 5pq
4. (a) What should be added to x2 +xy+y2 to obtain 2x2 +3xy ?
Answer
Let p should be added.
Then according to question,
x2 + xy + y2 + p = 2x2 + 3xy
⇒ p = 2x2 + 3xy - (x2 + xy + y2)
⇒ p = 2x2 + 3xy - x2 - xy - y2
⇒ p = 2x2 - x2- y2 +3xy - xy
⇒ p = x2 - y2 + 2xy
Hence, x2 - y2 + 2xy should be added.
(b) What should be subtracted from 2a + 8b+10 to get -3a + 7b + 16?
Answer
Let q should be subtracted.
Then according to question, 2a + 8b + 10-q = -3a + 7b + 16
⇒ -q = -3a +7b + 16 - (2a + 8b + 10)
⇒ -q = -3a + 7b + 16 - 2a - 8b - 10
⇒ - q = -3a - 2a + 7b - 8b + 16 - 10
⇒ -q = -5a - b + 6
⇒ q = - (- 5a - b + -6)
⇒ q = 5a + b - 6
5. What should be taken away from 3x2- 4y2 + 5xy + 20 to obtain - x2 - y2 + 6xy + 20 ?
Answer
Let q should be subtracted.
Then according to question,
3x2 - 4y2 + 5xy + 20 -q = -x2 - y2 + 6xy + 20
⇒ q = 3x2 - 4y2 + 5xy + 20 - (-x2 - y2 + 6xy + 20)
⇒ q = 3x2 - 4y2 + 5xy+ 20 + x2 + y2 - 6xy - 20
⇒ q = 3x2 + x2 - 4y2 +y2 + 5xy - 6xy + 20-20
⇒ q = 4x2 - 3y2 - xy + 0
Hence, 4x2 -3y2 -xy should be subtracted.
6. (a) From the sum of 3x - y + 11 and - y - 11, subtract 3x - y - 11.
Answer
First we have to find out the sum of 3x – y + 11 and – y – 11
= 3x – y + 11 + (-y - 11)
= 3x – y + 11 – y – 11
= 3x – y – y + 11 – 11
= 3x – 2y
Now, subtract 3x – y – 11 from 3x – 2y
= 3x – 2y – (3x – y - 11)
= 3x – 2y – 3x + y + 11
= 3x – 3x – 2y + y + 11
= -y + 11
(b) From the sum of 4 + 3x and 5 - 4x + 2x2, subtract the sum of 3x2 - 5x and -x2 + 2x + 5.
Answer
First we have to find out the sum of 4 + 3x and 5 – 4x + 2x2
= 4 + 3x + (5 – 4x + 2x2)
= 4 + 3x + 5 – 4x + 2x2
= 4 + 5 + 3x – 4x + 2x2
= 9 - x + 2x2
= 2x2– x + 9 … [equation 1]
Then, we have to find out the sum of 3x2– 5x and – x2 + 2x + 5.
Exercise 12.3
1. If m = 2, find the value of:
(i) m - 2
(ii) 3m - 5
(iii) 9 - 5m
(iv) 3m2 - 2m - 7
(v) ![]()
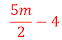
Answer
(i) m - 2 = 2 - 2 [Putting m = 2]
= 0
(ii) 3m - 5 = 3 x 2 - 5 [Putting m = 2]
= 6 - 5 = 1
(iii) 9 - 5m = 9 - 5 x 2 [Putting m = 2]
= 9 - 10 = - 1
(iv) 3m2 - 2m - 7
= 3(2)2 - 2 (2) - 7 [Putting m = 2]
=3 × 4 - 2 × 2 - 7
= 12-4-7
= 12- 11 = 1
(v) ![]()
[Putting m = 2]
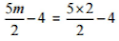[Putting m = 2]= 5 - 4 = 1
2. If p = -2, find the value of:
(i) 4p + 7
(ii) - 3p2 + 4p + 7
(iii) -2p3 - 3p2 +4/7 + 7
Answer
(i) 4p + 7 = 4 (- 2) + 7 [Putting p= -2]
= -8 + 7 = -1
(ii) -3p2+4p + 7
= -3 (-2)2+ 4 (-2) + 7 [Putting p = - 2]
= - 3 × 4 - 8 + 7
= - 12 - 8 + 7
= -20 + 7 = -13
(iii) - 2p3 - 3p2 +4p + 7
= - 2 (-2)3 - 3(-2)2 + 4 (-2) + 7 [Putting p = - 2]
= -2 ×(-8)-3 ×4 -8 + 7
= 16-12-8 + 7
= -20 + 23 = 3
3. Find the value of the following expressions, when x = -1:
(i) 2x - 7
(ii) -x + 2
(iii) x2 + 2x + 1
(iv) 2x2- x - 2
Answer
(i) 2x - 7 = 2 (-1) - 7 [Putting x= - 1]
= - 2 - 7 = - 9
(ii) - x + 2 = - (-1) + 2 [Putting x= - 1]
= 1 + 2 = 3
(iii) x2 + 2 x + 1 = (-1)2 + 2 (-1) + 1 [Putting x= - 1]
= 1 - 2 + 1
= 2 - 2 = 0
(iv) 2x2- x - 2 = 2 (-1)2 - (-1) - 2 [Putting x= - 1]
= 2x 1 + 1-2
= 2 + 1 - 2
= 3 - 2 = 1
4. If a = 2,b = -2, find the value of:
(i) a2 + b2
(ii) a2+ab + b2
(iii) a2 - b2
Answer
(i) a2 + b2 ( 2)2 + (- 2)2 [Putting a = 2. b = - 2 ]
= 4 + 4 = 8
(ii) a2+ab + b2
= (2) + ( 2) (- 2) +(-2)2 [Putting a = 2. b = - 2 ]
= 4 - 4 + 4 = 4
(iii) a2 - b2 = (2)2 - (-2)2 [Putting a = 2,b = - 2]
= 4 - 4 = 0
5. When a = 0, b = -1, find the value of the given expressions:
(i) 2a + 2b
(ii) 2a2+b2+1
(iii) 2a2b + 2ab2 +ab
(iv) a2+ab+2
Answer
(i) 2a + 2b = 2 (0) + 2 (-1) [Putting a - 0,b = - 1]
= 0 - 2 = -2
(ii) 2a2 + b2 + 1 = 2 (0)2 + (-1)2 + 1 [Putting a - 0,b = - 1]
= 2 x 0 + 1+ 1 = 0 + 2 = 2
(iii) 2a2b + 2ab2 + ab = 2(0)2 (-1) + 2 (0 )(-1)2 + (0 )(-1) [Putting a - 0,b = - 1]
= 0 + 0 + 0 = 0
(iv) a2 +ab + 2 - (0)2 + (0) (-1) + 2 [Putting a - 0,b = - 1]
= 0 + 0 + 2 = 2
6. Simplify the expressions and find the value if x is equal to 2:
(i) x + 7 + 4 (x- 5)
(ii) 3 (x + 2) + 5x - 7
(iii) 6x + 5 (x - 2)
(iv) 4 (2x - 1) + 3x + 11
Answer
(i) x + 7 + 4(x- 5) = x + 7 + 4x - 20 = x + 4 x + 7 - 20
= 5 x - 13 = 5 x 2 - 13 [Putting x = 2]
= 10-13 = -3
(ii) 3 (x+ 2) + 5x - 7 = 3x + 6 + 5x -7 = 3x + 5x + 6 - 7
= 8x - 1 = 8 x 2-1 [Putting x = -1]
= 16 - 1 = 15
(iii) 6x + 5 (x - 2) = 6x + 5x -10 = 11x - 10
= 11 x 2 - 10 [Putting x = -1]
= 22 - 10 = 12
(iv) 4(2x - 1) + 3x + 11 = 8x - 4 + 3x +11 = 8x + 3a - 4 + 11
= 11a + 7 = 11 x 2 + 7 [Putting x = - 1]
= 22+7 = 29
7. Simplify these expressions and find their values if x = 3,a = -1, b = - 2 :
(i) 3x - 5 - x + 9
(ii) 2 - 8x + 4x + 4
(iii) 3a + 5 - 8a + 1
(iv) 10 - 3b - 4 - 5b
(v) 2a - 2b - 4 - 5 + a
Answer
(i) 3a - 5 - x + 9 = 3x - x - 5 + 9 = 2x + 4
= 2x3+4 [Putting a = 3]
= 6 + 4 = 10
(ii) 2 - 8x + 4x + 4 = - 8x + 4x + 2 + 4 = -4x + 6
= - 4 x 3 + 6 [Putting a = 3]
= -12 + 6 =12
(iii) 3a + 5 - 8a + 1 = 3a - 8a + 5 + 1 = - 5a + 6
= -5(- 1) + 6 [Putting a = - 1]
= 5 + 6 = 11
(iv) 10 - 3b - 4 - 5b = - 3b - 5b + 10 - 4 = -8b+6
= -8 (-2)+ 6 [Putting b = -2]
= 16 + 6 = 22
(v) 2a - 2b - 4 - 5 + a = 2a + a - 2b - 4 - 5
= 3a - 2b - 9 = 3 (-1)-2 (-2) -9 [Putting a = -1 , b = - 2]
= -3 + 4 -9 = -8
8. (i) If z = 10, find the value of z3 - 3 (z - 10).
(ii) If p = - 10, find the value of p2 - 2p - 100
Answer
(i) z3 -3(z-10) = (10)3-3(10 - 10) [Putting z = 10]
= 1000 - 3 x 0 = 1000- 0
= 1000
(ii) p2 - 2p - 100 = (-10)2 - 2 (-10) - 100 (Putting p = - 10]
= 100+ 20 - 100 = 20
9. What should be the value of a if the value of 2x2 + x - a equals to 5, when x = 0 ?
Answer
Given: 2x2 + x - a = 5
⇒ 2 (0)2 + 0 - a = 5 [Putting x = 0]
⇒ 0 + 0 - a = 5
⇒ a = -5
Hence, the value of a is -5.
10. Simplify the expression and find its value when a = 5 and b = - 3: 2 (a2 + ab) + 3 - ab
Answer
Given 2 (a2 + ab) + 3 - ab
⇒ 2a2 + 2ab + 3 - ab
⇒ 2a2 + 2ab - ab + 3
⇒ 2a2 + ab + 3
⇒ 2 (5)2 + (5) (-3) + 3 [Putting a = 5 , b = -3]
⇒ 2 x 25 - 15 + 3
⇒ 50 - 15 + 3
⇒ 38.